Câu hỏi: Cho hình chóp S.ABC có $SA\bot \left( ABC \right)$, tam giác ABC đều $AB=a$ ; góc giữa SB và mặt phẳng $\left( ABC \right)$ bằng $60{}^\circ $. Gọi M, N lần lượt là trung điểm của SA, SB. Tính thể tích khối chóp SMNC.
A. $\dfrac{{{a}^{3}}}{16}.$
B. $\dfrac{{{a}^{3}}}{4}.$
C. $\dfrac{{{a}^{3}}\sqrt{3}}{12}.$
D. $\dfrac{{{a}^{3}}}{8}.$
A. $\dfrac{{{a}^{3}}}{16}.$
B. $\dfrac{{{a}^{3}}}{4}.$
C. $\dfrac{{{a}^{3}}\sqrt{3}}{12}.$
D. $\dfrac{{{a}^{3}}}{8}.$
Lưu ý: Công thức tỉ số thể tích: $\dfrac{{{V}_{SMNC}}}{{{V}_{SABC}}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}.\dfrac{SC}{SC}$.
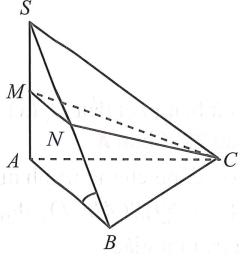
Ta có: $SA\bot \left( ABC \right)\Rightarrow \widehat{\left( SB,\left( ABC \right) \right)}=\widehat{\left( SB,AB \right)}=\widehat{SBA}=60{}^\circ $.
Xét tam giác vuông SAB: $SA=AB.\tan 60{}^\circ =a\sqrt{3}$.
$\Rightarrow {{V}_{S.ABC}}=\dfrac{1}{3}.SA.{{S}_{ABC}}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{{{a}^{2}}\sqrt{3}}{4}=\dfrac{{{a}^{3}}}{4}.$
Ta có: $\dfrac{{{V}_{SMNC}}}{{{V}_{SABC}}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}=\dfrac{1}{4}\Rightarrow {{V}_{SMNC}}=\dfrac{{{a}^{3}}}{16}.$
Ta có: $SA\bot \left( ABC \right)\Rightarrow \widehat{\left( SB,\left( ABC \right) \right)}=\widehat{\left( SB,AB \right)}=\widehat{SBA}=60{}^\circ $.
Xét tam giác vuông SAB: $SA=AB.\tan 60{}^\circ =a\sqrt{3}$.
$\Rightarrow {{V}_{S.ABC}}=\dfrac{1}{3}.SA.{{S}_{ABC}}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{{{a}^{2}}\sqrt{3}}{4}=\dfrac{{{a}^{3}}}{4}.$
Ta có: $\dfrac{{{V}_{SMNC}}}{{{V}_{SABC}}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}=\dfrac{1}{4}\Rightarrow {{V}_{SMNC}}=\dfrac{{{a}^{3}}}{16}.$
Đáp án A.