Google
Câu hỏi: Cho hình chóp $S.ABC$ có $SA\bot \left( ABC \right)$ , $AB=3, AC=2$ và $\widehat{BAC}=60{}^\circ $. Gọi $M, N$ lần lượt là hình chiếu của $A$ lên $SB, SC$. Tính bán kính $R$ mặt cầu ngoại tiếp hình chóp $A.BCNM$.
A. $R=\sqrt{2}$.
B. $R=\dfrac{\sqrt{21}}{3}$.
C. $R=\dfrac{4}{\sqrt{3}}$.
D. $R=1$.
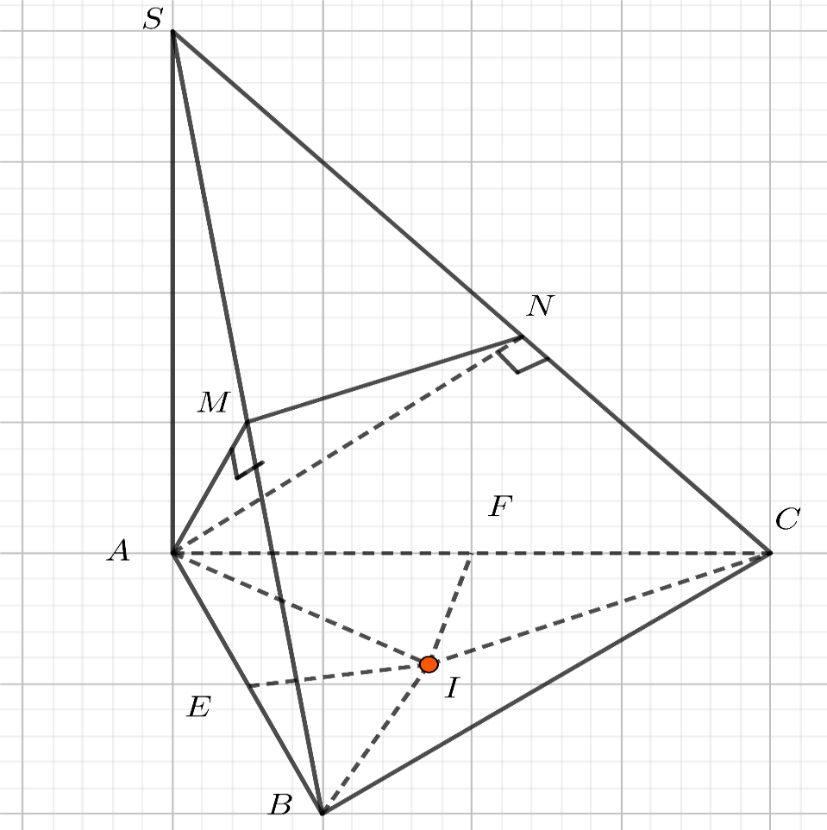Gọi $I$ là tâm đường tròn ngoại tiếp tam giác $ABC\Rightarrow IA=IB=IC$.
Gọi $E, F$ lần lượt là trung điểm của $AB, AC$.
Ta có $\left\{ \begin{aligned}
& IE\bot AB \\
& IE\bot SA\left( do SA\bot \left( ABC \right), IE\subset \left( ABC \right) \right) \\
\end{aligned} \right.\Rightarrow IE\bot \left( SAB \right) hay IE\bot \left( MAB \right)$.
Mặt khác tam giác $MAB$ vuông tại $M$ nên $E$ là tâm đường tròn ngoại tiếp tam giác $MAB$.
Do vậy $IE$ là trục của đường tròn ngoại tiếp tam giác $MAB\Rightarrow IM=IA=IB$ $\left( * \right)$ .
Tương tự có $IF$ là trục của đường tròn ngoại tiếp tam giác $NAC\Rightarrow IN=IA=IC \left( ** \right)$.
Từ $\left( * \right)$ và $\left( ** \right)$ $IA=IB=IC=IN=IM\Rightarrow I$ là tâm của mặt cầu ngoại tiếp hình chóp $A.BCNM$.
Bán kính mặt cầu $R=IA=\dfrac{AB.BC.AC}{4S{}_{\Delta ABC}}$.
Có ${{S}_{\Delta ABC}}=\dfrac{1}{2}.AB.AB.sinA=\dfrac{1}{2}.2.3.\sin 60=\dfrac{3\sqrt{3}}{2}$.
Lại có $BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}-2.AB.AC.cosA}=\sqrt{{{3}^{2}}+{{2}^{2}}-2.3.2.\cos 60{}^\circ }=\sqrt{7}$
Do vậy $R=\dfrac{3.2.\sqrt{7}}{4.\dfrac{3\sqrt{3}}{2}}=\dfrac{\sqrt{21}}{3}$.
A. $R=\sqrt{2}$.
B. $R=\dfrac{\sqrt{21}}{3}$.
C. $R=\dfrac{4}{\sqrt{3}}$.
D. $R=1$.
Gọi $E, F$ lần lượt là trung điểm của $AB, AC$.
Ta có $\left\{ \begin{aligned}
& IE\bot AB \\
& IE\bot SA\left( do SA\bot \left( ABC \right), IE\subset \left( ABC \right) \right) \\
\end{aligned} \right.\Rightarrow IE\bot \left( SAB \right) hay IE\bot \left( MAB \right)$.
Mặt khác tam giác $MAB$ vuông tại $M$ nên $E$ là tâm đường tròn ngoại tiếp tam giác $MAB$.
Do vậy $IE$ là trục của đường tròn ngoại tiếp tam giác $MAB\Rightarrow IM=IA=IB$ $\left( * \right)$ .
Tương tự có $IF$ là trục của đường tròn ngoại tiếp tam giác $NAC\Rightarrow IN=IA=IC \left( ** \right)$.
Từ $\left( * \right)$ và $\left( ** \right)$ $IA=IB=IC=IN=IM\Rightarrow I$ là tâm của mặt cầu ngoại tiếp hình chóp $A.BCNM$.
Bán kính mặt cầu $R=IA=\dfrac{AB.BC.AC}{4S{}_{\Delta ABC}}$.
Có ${{S}_{\Delta ABC}}=\dfrac{1}{2}.AB.AB.sinA=\dfrac{1}{2}.2.3.\sin 60=\dfrac{3\sqrt{3}}{2}$.
Lại có $BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}-2.AB.AC.cosA}=\sqrt{{{3}^{2}}+{{2}^{2}}-2.3.2.\cos 60{}^\circ }=\sqrt{7}$
Do vậy $R=\dfrac{3.2.\sqrt{7}}{4.\dfrac{3\sqrt{3}}{2}}=\dfrac{\sqrt{21}}{3}$.
Đáp án B.