Google
Câu hỏi: Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ vuông tại $A$, $AB=a,BC=2a$ và $SB$ vuông góc với mặt phẳng $\left( ABC \right)$. Biết góc giữa hai mặt phẳng $\left( SAC \right)$ và $\left( SBC \right)$ bẳng $60{}^\circ $. Thể tích của khối chóp $S.ABC$ bằng
A. $\dfrac{{{a}^{3}}\sqrt{2}}{6}$.
B. $\dfrac{{{a}^{3}}\sqrt{6}}{12}$.
C. $\dfrac{{{a}^{3}}\sqrt{6}}{4}$.
D. $\dfrac{{{a}^{3}}\sqrt{2}}{2}$.
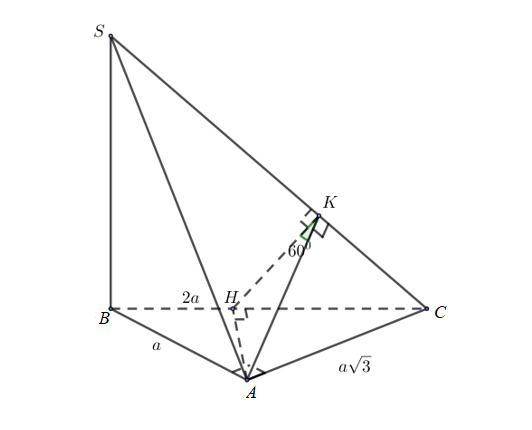Trong $\Delta ABC$ kẻ $AH\bot BC$. Ta có: $\left\{ \begin{aligned}
& AH\bot BC \\
& SB\bot AH \\
\end{aligned} \right.$$\Rightarrow AH\bot \left( SBC \right) $ $ \Rightarrow AH\bot SC\left( 1 \right)$.
Trong $\Delta SAC$ kẻ $AK\bot SC$ $\left( 2 \right)$.
Từ $\left( 1 \right),\left( 2 \right)$ $\Rightarrow SC\bot \left( AKH \right)$ $\Rightarrow SC\bot HK$.
Góc giữa hai mặt phẳng $\left( SAC \right)$ và $\left( SBC \right)$ là $\widehat{AKH}$ nên $\widehat{AKH}=60{}^\circ $.
Ta có: $AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=a\sqrt{3}$,
$A{{C}^{2}}=CH.BC\Rightarrow CH=\dfrac{A{{C}^{2}}}{BC}=\dfrac{3{{a}^{2}}}{2a}=\dfrac{3a}{2}$,
$\Rightarrow AH=\sqrt{A{{C}^{2}}-C{{H}^{2}}}=\dfrac{a\sqrt{3}}{2}$.
Trong $\Delta AKH$ vuông tại $H$ có $HK=AH.\cot 60{}^\circ =\dfrac{a}{2}$, $CK=\sqrt{C{{H}^{2}}-H{{K}^{2}}}=a\sqrt{2}$.
$\Delta SBC\backsim \Delta HKC\left( g.g \right)$ nên $\dfrac{SB}{HK}=\dfrac{BC}{KC}=\dfrac{2a}{a\sqrt{2}}=\sqrt{2}$ $\Rightarrow SB=HK.\sqrt{2}=\dfrac{a}{\sqrt{2}}$
Thể tích hình chóp $S.ABC$ là $V=\dfrac{1}{3}SB.{{S}_{\Delta ABC}}$ $=\dfrac{1}{3}\dfrac{a}{\sqrt{2}}.\dfrac{1}{2}.a.\sqrt{3}.a=\dfrac{{{a}^{3}}\sqrt{6}}{12}$.
A. $\dfrac{{{a}^{3}}\sqrt{2}}{6}$.
B. $\dfrac{{{a}^{3}}\sqrt{6}}{12}$.
C. $\dfrac{{{a}^{3}}\sqrt{6}}{4}$.
D. $\dfrac{{{a}^{3}}\sqrt{2}}{2}$.
& AH\bot BC \\
& SB\bot AH \\
\end{aligned} \right.$$\Rightarrow AH\bot \left( SBC \right) $ $ \Rightarrow AH\bot SC\left( 1 \right)$.
Trong $\Delta SAC$ kẻ $AK\bot SC$ $\left( 2 \right)$.
Từ $\left( 1 \right),\left( 2 \right)$ $\Rightarrow SC\bot \left( AKH \right)$ $\Rightarrow SC\bot HK$.
Góc giữa hai mặt phẳng $\left( SAC \right)$ và $\left( SBC \right)$ là $\widehat{AKH}$ nên $\widehat{AKH}=60{}^\circ $.
Ta có: $AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=a\sqrt{3}$,
$A{{C}^{2}}=CH.BC\Rightarrow CH=\dfrac{A{{C}^{2}}}{BC}=\dfrac{3{{a}^{2}}}{2a}=\dfrac{3a}{2}$,
$\Rightarrow AH=\sqrt{A{{C}^{2}}-C{{H}^{2}}}=\dfrac{a\sqrt{3}}{2}$.
Trong $\Delta AKH$ vuông tại $H$ có $HK=AH.\cot 60{}^\circ =\dfrac{a}{2}$, $CK=\sqrt{C{{H}^{2}}-H{{K}^{2}}}=a\sqrt{2}$.
$\Delta SBC\backsim \Delta HKC\left( g.g \right)$ nên $\dfrac{SB}{HK}=\dfrac{BC}{KC}=\dfrac{2a}{a\sqrt{2}}=\sqrt{2}$ $\Rightarrow SB=HK.\sqrt{2}=\dfrac{a}{\sqrt{2}}$
Thể tích hình chóp $S.ABC$ là $V=\dfrac{1}{3}SB.{{S}_{\Delta ABC}}$ $=\dfrac{1}{3}\dfrac{a}{\sqrt{2}}.\dfrac{1}{2}.a.\sqrt{3}.a=\dfrac{{{a}^{3}}\sqrt{6}}{12}$.
Đáp án B.