Google
Câu hỏi: Cho hình chóp đều $S.ABC$ có $\widehat{ASB}=30{}^\circ $. Một mặt phẳng thay đổi qua $A$ cắt các cạnh $SB$ và $SC$ lần lượt tại $M$ và $N$. Tính tỉ số thể tích của các khối chóp $S.AMN$ và $S.ABC$ khi chu vi tam giác $AMN$ đạt giá trị nhỏ nhất.
A. $2\left( \sqrt{3}-1 \right).$
B. $\dfrac{3+\sqrt{2}}{5}.$
C. $\dfrac{3\left( \sqrt{3}-1 \right)}{4}.$
D. $2\left( 2-\sqrt{3} \right).$
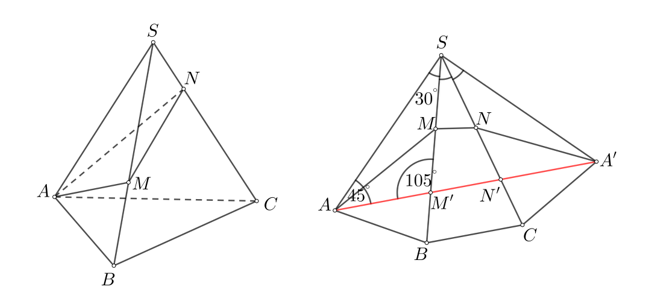Trải các mặt của hình chóp $S.ABC$ trên cùng một mặt phẳng $\left( SBC \right)$ như hình vẽ trên.
Ta có $AM+MN+NA=AM+MN+N{A}'\ge A{A}'$.
Dấu $''=''$ xảy ra khi và chỉ khi $A,M,N,{A}'$ thẳng hàng.
Vậy chu vi tam giác $AMN$ nhỏ nhất khi $M,N$ lần lượt là các giao điểm của $A{A}'$ với $SB,SC$.
Ta có tam giác $SA{A}'$ cân tại $S$ và $\widehat{AS{A}'}=90{}^\circ $ nên $\widehat{SA{A}'}=\widehat{S{A}'A}=45{}^\circ $.
Suy ra $\vartriangle SAM=\vartriangle S{A}'N(\text{g-c-g})$, từ đó $SM=SN$.
Mặt khác $\dfrac{SM}{SA}=\dfrac{\sin \widehat{SAM}}{\sin \widehat{SMA}}=\dfrac{\sin 45{}^\circ }{\sin 105{}^\circ }=\sqrt{3}-1$.
Nên $\dfrac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\dfrac{SM}{SB}.\dfrac{SN}{SC}={{\left( \sqrt{3}-1 \right)}^{2}}=2\left( 2-\sqrt{3} \right)$.
A. $2\left( \sqrt{3}-1 \right).$
B. $\dfrac{3+\sqrt{2}}{5}.$
C. $\dfrac{3\left( \sqrt{3}-1 \right)}{4}.$
D. $2\left( 2-\sqrt{3} \right).$
Ta có $AM+MN+NA=AM+MN+N{A}'\ge A{A}'$.
Dấu $''=''$ xảy ra khi và chỉ khi $A,M,N,{A}'$ thẳng hàng.
Vậy chu vi tam giác $AMN$ nhỏ nhất khi $M,N$ lần lượt là các giao điểm của $A{A}'$ với $SB,SC$.
Ta có tam giác $SA{A}'$ cân tại $S$ và $\widehat{AS{A}'}=90{}^\circ $ nên $\widehat{SA{A}'}=\widehat{S{A}'A}=45{}^\circ $.
Suy ra $\vartriangle SAM=\vartriangle S{A}'N(\text{g-c-g})$, từ đó $SM=SN$.
Mặt khác $\dfrac{SM}{SA}=\dfrac{\sin \widehat{SAM}}{\sin \widehat{SMA}}=\dfrac{\sin 45{}^\circ }{\sin 105{}^\circ }=\sqrt{3}-1$.
Nên $\dfrac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\dfrac{SM}{SB}.\dfrac{SN}{SC}={{\left( \sqrt{3}-1 \right)}^{2}}=2\left( 2-\sqrt{3} \right)$.
Đáp án D.