Google
Câu hỏi: Cho hình chóp $S.ABC$ có $SA=SB=SC=2,$ $\widehat{ASB}={{90}^{\circ }},$ $\widehat{BSC}={{60}^{\circ }},$ $\widehat{CSA}={{120}^{\circ }}.$ Diện tích mặt cầu ngoại tiếp hình chóp bằng:
A. $4\pi $.
B. $\dfrac{16\pi }{3}$.
C. $16\pi $.
D. $8\pi $.
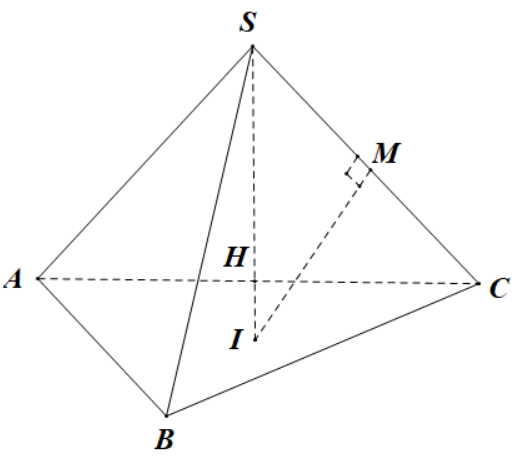Ta có $SB=SC=2$, $\widehat{BSC}=60{}^\circ $ suy ra tam giác $BSC$ đều $\Rightarrow BC=2$.
Lại có $SA=SC=2$, $\widehat{ASB}=90{}^\circ $ suy ra tam giác $ASB$ vuông cân tại $S$ $\Rightarrow AB=2\sqrt{2}$.
Mặt khác, $SA=SC=2$, $\widehat{ASB}=120{}^\circ $, áp dụng định lí cosin cho tam giác $ASC$, ta được:
$A{{C}^{2}}=S{{A}^{2}}+S{{C}^{2}}-2SA.SC.cos\widehat{ASC}={{3.2}^{2}}\Leftrightarrow AC=2\sqrt{3}$.
Xét tam giác $ABC$ có $B{{C}^{2}}+A{{B}^{2}}={{2}^{2}}+{{\left( 2\sqrt{2} \right)}^{2}}=12=A{{C}^{2}}$ suy ra tam giác $ABC$ vuông tại $B$.
Gọi $H$ là trung điểm của cạnh $AC$ suy ra $H$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
Mà $SA=SB=SC$ $\Rightarrow SH\bot \left( ABC \right)$.
Trong mặt phẳng $\left( SAC \right)$ kẻ đường trung trực canh $SC$ cắt đường thẳng $SH$ tại $I$ suy ra là tâm mặt cầu ngoại tiếp hình chóp.
Xét tam giác vuông $ASH$ vuông tại $H$ có $SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{2}^{2}}-{{\left( \dfrac{2\sqrt{3}}{2} \right)}^{2}}}=1$.
Ta có $\Delta SHC\sim \Delta SMI\Rightarrow \dfrac{SI}{SC}=\dfrac{SM}{SH}\Leftrightarrow SI=\dfrac{SM.SC}{SH}=2$
Diện tích mặt cầu ngoại tiếp chóp là. $S=4\pi {{R}^{2}}=16\pi $.
A. $4\pi $.
B. $\dfrac{16\pi }{3}$.
C. $16\pi $.
D. $8\pi $.
Lại có $SA=SC=2$, $\widehat{ASB}=90{}^\circ $ suy ra tam giác $ASB$ vuông cân tại $S$ $\Rightarrow AB=2\sqrt{2}$.
Mặt khác, $SA=SC=2$, $\widehat{ASB}=120{}^\circ $, áp dụng định lí cosin cho tam giác $ASC$, ta được:
$A{{C}^{2}}=S{{A}^{2}}+S{{C}^{2}}-2SA.SC.cos\widehat{ASC}={{3.2}^{2}}\Leftrightarrow AC=2\sqrt{3}$.
Xét tam giác $ABC$ có $B{{C}^{2}}+A{{B}^{2}}={{2}^{2}}+{{\left( 2\sqrt{2} \right)}^{2}}=12=A{{C}^{2}}$ suy ra tam giác $ABC$ vuông tại $B$.
Gọi $H$ là trung điểm của cạnh $AC$ suy ra $H$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
Mà $SA=SB=SC$ $\Rightarrow SH\bot \left( ABC \right)$.
Trong mặt phẳng $\left( SAC \right)$ kẻ đường trung trực canh $SC$ cắt đường thẳng $SH$ tại $I$ suy ra là tâm mặt cầu ngoại tiếp hình chóp.
Xét tam giác vuông $ASH$ vuông tại $H$ có $SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{2}^{2}}-{{\left( \dfrac{2\sqrt{3}}{2} \right)}^{2}}}=1$.
Ta có $\Delta SHC\sim \Delta SMI\Rightarrow \dfrac{SI}{SC}=\dfrac{SM}{SH}\Leftrightarrow SI=\dfrac{SM.SC}{SH}=2$
Diện tích mặt cầu ngoại tiếp chóp là. $S=4\pi {{R}^{2}}=16\pi $.
Đáp án C.