Câu hỏi: Chứng minh công thức
\(\cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \)
(với \(0 < \beta < \dfrac{\pi }{2}\)) bằng “phương pháp hình học” như sau:
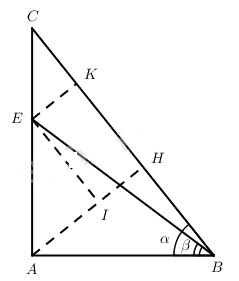
Xét tam giác vuông ABC với \(\widehat A = \dfrac{\pi }{2};\widehat {ABC} = \alpha ;\) E là một điểm trên AC sao cho \(\widehat {ABE} = \beta \). Kẻ AH, EK vuông góc với BC (h. 6.8) thì dễ thấy \(\cos \left( {\alpha - \beta } \right) = \dfrac{{BK}}{{BE}} = \dfrac{{BH}}{{BE}} + \dfrac{{HK}}{{BE}}\). Từ đó suy ra công thức trên.
\(\cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \)
(với \(0 < \beta < \dfrac{\pi }{2}\)) bằng “phương pháp hình học” như sau:
Xét tam giác vuông ABC với \(\widehat A = \dfrac{\pi }{2};\widehat {ABC} = \alpha ;\) E là một điểm trên AC sao cho \(\widehat {ABE} = \beta \). Kẻ AH, EK vuông góc với BC (h. 6.8) thì dễ thấy \(\cos \left( {\alpha - \beta } \right) = \dfrac{{BK}}{{BE}} = \dfrac{{BH}}{{BE}} + \dfrac{{HK}}{{BE}}\). Từ đó suy ra công thức trên.

Lời giải chi tiết
Ta có:
\(\cos \left( {\alpha - \beta } \right) = \dfrac{{BK}}{{BE}} = \dfrac{{BH}}{{BE}} + \dfrac{{HK}}{{BE}}\)
\(= \dfrac{{BH}}{{BA}}.\dfrac{{BA}}{{BE}} + \dfrac{{EJ}}{{BE}}\) (HKEJ là hình chữ nhật)
\(\dfrac{{BH}}{{BA}}.\dfrac{{BA}}{{BE}} + \dfrac{{EJ}}{{EA}}.\dfrac{{EA}}{{BE}} = \cos \alpha \cos \beta + \sin \alpha \sin \beta .\)
Ta có:
\(\cos \left( {\alpha - \beta } \right) = \dfrac{{BK}}{{BE}} = \dfrac{{BH}}{{BE}} + \dfrac{{HK}}{{BE}}\)
\(= \dfrac{{BH}}{{BA}}.\dfrac{{BA}}{{BE}} + \dfrac{{EJ}}{{BE}}\) (HKEJ là hình chữ nhật)
\(\dfrac{{BH}}{{BA}}.\dfrac{{BA}}{{BE}} + \dfrac{{EJ}}{{EA}}.\dfrac{{EA}}{{BE}} = \cos \alpha \cos \beta + \sin \alpha \sin \beta .\)