Câu hỏi: Cho hình chóp S. ABCD có đáy là tam giác không cân và SA vuông góc với mp(ABC). Gọi AB1, AC1 lần lượt là các đường cao của tam giác SAB và SAC.
a) Chứng minh rằng B1C1 và BC là hai đường thẳng cắt nhau.
b) Gọi I là giao điểm của hai đường thẳng BC và B1C1. Chứng minh rằng \(\widehat {IAB} = \widehat {IC{\rm{A}}}\).
a) Chứng minh rằng B1C1 và BC là hai đường thẳng cắt nhau.
b) Gọi I là giao điểm của hai đường thẳng BC và B1C1. Chứng minh rằng \(\widehat {IAB} = \widehat {IC{\rm{A}}}\).
Lời giải chi tiết
a)
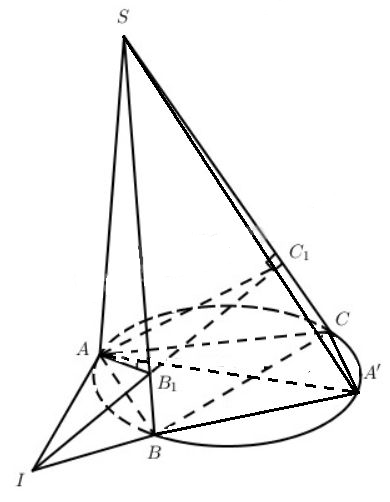
Ta có \(S{A^2} = SB. S{B_1} = SC. S{C_1}\).
Vậy bốn điểm B, C, B1, C1 thuộc một đường tròn, Nếu B1C1 và BC là hai đường thẳng song song thì suy ra BB1C1C là hình thang cân, từ đó SBC là tam giác cân tại S, điều đó dẫn đến ABC là tam giác cân tại A, mâu thuẫn với giả thiết, từ đó suy ra điều phải chứng minh.
b)
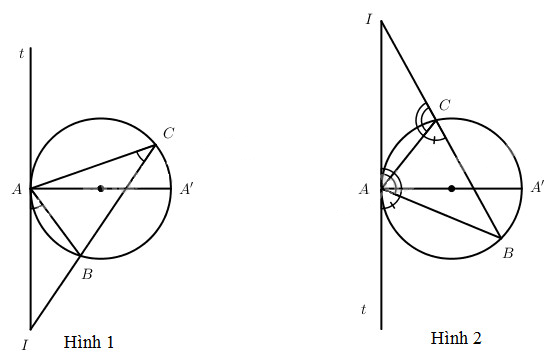
Gọi I là giao điểm của B1C1 và BC thì AI là giao tuyến của (ABC) và (AB1C1). Gọi AA’ là đường kính của đường tròn ngoại tiếp tam giác ABC thì ta chứng minh được \(\left( {A{B_1}{C_1}} \right) \bot SA'\), từ đó \(AI \bot AA'\). Như vậy, giao tuyến AI là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
Nếu điểm B nằm giữa I và C (hình 1) thì ta có \(\widehat {IAB} = \widehat {IC{\rm{A}}}\) (cùng chắn cung AB).
Nếu điểm C nằm giữa I và B (hình 2) thì ta có:
\(\widehat {BAt} = \widehat {ABC}\) (cùng chắn cung AB);
mặt khác \(\widehat {IAB} + \widehat {BAt} = {180^0}\)
và \(\widehat {IC{\rm{A}}} + \widehat {ACB} = {180^0}\)
Như vậy \(\widehat {IC{\rm{A}}} = \widehat {IAB}\).
a)
Ta có \(S{A^2} = SB. S{B_1} = SC. S{C_1}\).
Vậy bốn điểm B, C, B1, C1 thuộc một đường tròn, Nếu B1C1 và BC là hai đường thẳng song song thì suy ra BB1C1C là hình thang cân, từ đó SBC là tam giác cân tại S, điều đó dẫn đến ABC là tam giác cân tại A, mâu thuẫn với giả thiết, từ đó suy ra điều phải chứng minh.
b)
Gọi I là giao điểm của B1C1 và BC thì AI là giao tuyến của (ABC) và (AB1C1). Gọi AA’ là đường kính của đường tròn ngoại tiếp tam giác ABC thì ta chứng minh được \(\left( {A{B_1}{C_1}} \right) \bot SA'\), từ đó \(AI \bot AA'\). Như vậy, giao tuyến AI là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
Nếu điểm B nằm giữa I và C (hình 1) thì ta có \(\widehat {IAB} = \widehat {IC{\rm{A}}}\) (cùng chắn cung AB).
Nếu điểm C nằm giữa I và B (hình 2) thì ta có:
\(\widehat {BAt} = \widehat {ABC}\) (cùng chắn cung AB);
mặt khác \(\widehat {IAB} + \widehat {BAt} = {180^0}\)
và \(\widehat {IC{\rm{A}}} + \widehat {ACB} = {180^0}\)
Như vậy \(\widehat {IC{\rm{A}}} = \widehat {IAB}\).