Câu hỏi: Chứng minh rằng nếu các cặp cạnh đối diện của tứ diện ABCD vuông góc với nhau từng đôi một thì trong bốn mặt của tứ diện có ít nhất một mặt là tam giác nhọn (cả ba góc của nó đều nhọn).
Lời giải chi tiết
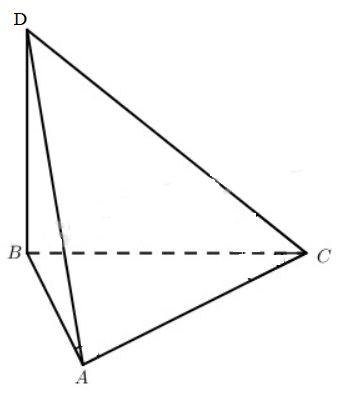
Giả sử ABCD là tứ diện có tính chất \(AB \bot C{\rm{D}}, AC \bot B{\rm{D}}, A{\rm{D}} \bot BC\).
Ta có:
\(A{B^2} + C{{\rm{D}}^2} = A{C^2} + B{{\rm{D}}^2} = B{C^2} + A{{\rm{D}}^2}\).
Từ đó, ta có
\(\eqalign{ & A{B^2} + A{C^2} - B{C^2} \cr & = A{C^2} + A{{\rm{D}}^2} - C{{\rm{D}}^2} \cr & = A{{\rm{D}}^2} + A{B^2} - B{{\rm{D}}^2} \cr} \)
Hệ thức này khẳng định các góc \(\widehat {BAC},\widehat {CA{\rm{D}}},\widehat {DAB}\) hoặc cùng nhọn, cùng vuông hoặc cùng tù.
Tương tự như trên, ta chứng minh được góc tại bất cứ đỉnh nào của tứ diện ABCD cũng có tính chất đó. Do tính chất tổng các góc trong của một tam giác bằng 1800 nên tồn tại nhiều nhất một đỉnh của tứ diện mà tại đó ba góc cùng vuông hay cùng tù. Khi ấy mặt đối diện với đỉnh đó của tứ diện ABCD có cả ba góc đều nhọn.
Vậy nên \(AB \bot C{\rm{D}}, AC \bot B{\rm{D}}\) và \(A{\rm{D}} \bot BC\) thì trong bốn mặt của tứ diện ABCD có ít nhất một mặt là tam giác nhọn (cả ba góc của nó nhỏ hơn 90°).
Giả sử ABCD là tứ diện có tính chất \(AB \bot C{\rm{D}}, AC \bot B{\rm{D}}, A{\rm{D}} \bot BC\).
Ta có:
\(A{B^2} + C{{\rm{D}}^2} = A{C^2} + B{{\rm{D}}^2} = B{C^2} + A{{\rm{D}}^2}\).
Từ đó, ta có
\(\eqalign{ & A{B^2} + A{C^2} - B{C^2} \cr & = A{C^2} + A{{\rm{D}}^2} - C{{\rm{D}}^2} \cr & = A{{\rm{D}}^2} + A{B^2} - B{{\rm{D}}^2} \cr} \)
Hệ thức này khẳng định các góc \(\widehat {BAC},\widehat {CA{\rm{D}}},\widehat {DAB}\) hoặc cùng nhọn, cùng vuông hoặc cùng tù.
Tương tự như trên, ta chứng minh được góc tại bất cứ đỉnh nào của tứ diện ABCD cũng có tính chất đó. Do tính chất tổng các góc trong của một tam giác bằng 1800 nên tồn tại nhiều nhất một đỉnh của tứ diện mà tại đó ba góc cùng vuông hay cùng tù. Khi ấy mặt đối diện với đỉnh đó của tứ diện ABCD có cả ba góc đều nhọn.
Vậy nên \(AB \bot C{\rm{D}}, AC \bot B{\rm{D}}\) và \(A{\rm{D}} \bot BC\) thì trong bốn mặt của tứ diện ABCD có ít nhất một mặt là tam giác nhọn (cả ba góc của nó nhỏ hơn 90°).