Câu hỏi: Các điểm \(A'(-4; 1), B'(2; 4), C'(2, -2)\) lần lượt là trung điểm của các cạnh \(BC, CA\) và \(AB\) của tam giác \(ABC\). Tính tọa độ đỉnh của tam giác \(ABC\). Chứng minh rằng trọng tâm tam giác \(ABC\) và \(A'B'C'\) trùng nhau.
Phương pháp giải
+) \(I\) là trung điểm của \(AB\) thì: \(\left\{ \begin{array}{l}
{x_I} = \frac{{{x_A} + {x_B}}}{2}\\
{y_I} = \frac{{{y_A} + {y_B}}}{2}
\end{array} \right..\)
+) \(G\) là trọng tâm tam giác \(ABC\) thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right..\)
Lời giải chi tiết
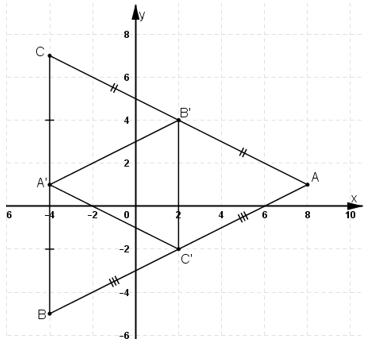
Giả sử \(A({x_A};{y_A}), B({x_B};{y_B}), C({x_C};{y_C})\)
\(A'\) là trung điểm BC \(\Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = \frac{{{x_B} + {x_C}}}{2}\\{y_{A'}} = \frac{{{y_B} + {y_C}}}{2}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l} - 4 = \frac{{{x_B} + {x_C}}}{2}\\1 = \frac{{{y_B} + {y_C}}}{2}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = - 8 \left( 1 \right)\\{y_B} + {y_C} = 2 \left(2 \right)\end{array} \right.\)
\(B'\) là trung điểm CA \(\Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = \frac{{{x_C} + {x_A}}}{2}\\{y_{B'}} = \frac{{{y_C} + {y_A}}}{2}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}2 = \frac{{{x_C} + {x_A}}}{2}\\4 = \frac{{{y_C} + {y_A}}}{2}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_C} + {x_A} = 4 \left( 3 \right)\\{y_C} + {y_A} = 8 \left(4 \right)\end{array} \right.\)
\(C'\) là trung điểm AB \(\Leftrightarrow \left\{ \begin{array}{l}{x_{C'}} = \frac{{{x_A} + {x_B}}}{2}\\{y_{C'}} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}2 = \frac{{{x_A} + {x_B}}}{2}\\ - 2 = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 4 \left( 5 \right)\\{y_A} + {y_B} = - 4 \left(6 \right)\end{array} \right.\)
Từ (1), (3) và (5) ta có hệ:
\(\left\{ \begin{array}{l}{x_B} + {x_C} = - 8\\{x_C} + {x_A} = 4\\{x_A} + {x_B} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = - 8 - {x_B}\\ - 8 - {x_B} + {x_A} = 4\\{x_A} + {x_B} = 4\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_C} = - 8 - {x_B}\\{x_A} - {x_B} = 12\\{x_A} + {x_B} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 8\\{x_B} = - 4\\{x_C} = - 4\end{array} \right.\)
Từ (2), (4) và (6) ta có hệ:
\(\left\{ \begin{array}{l}{y_B} + {y_C} = 2\\{y_C} + {y_A} = 8\\{y_A} + {y_B} = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_C} = 2 - {y_B}\\2 - {y_B} + {y_A} = 8\\{y_A} + {y_B} = - 4\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{y_C} = 2 - {y_B}\\{y_A} - {y_B} = 6\\{y_A} + {y_B} = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 1\\{y_B} = - 5\\{y_C} = 7\end{array} \right.\)
Vậy \(A\left( {8; 1} \right), B\left({ - 4; - 5} \right), C\left({ - 4; 7} \right)\).
Gọi \(G({x_G}; y{}_G)\) là trọng tâm của tam giác \(ABC\)
Khi đó ta có:
\(\left\{ \matrix{
{x_G} = {{{x_A} + {x_B} + {x_C}} \over 3} = {{8 - 4 - 4} \over 3} = 0 \hfill \cr
{y_G} = {{{y_A} + {y_B} + y{}_C} \over 3} = {{1 - 5 + 7} \over 3} = {1} \hfill \cr} \right.\)
Vậy \(G(0; 1)\) (*)
Gọi \(G'({x_{G'}}; y{}_{G'})\) là trọng tâm của tam giác \(A'B'C'\)
Khi đó ta có:
\(\left\{ \matrix{
{x_{G'}} = {{{x_{A'}} + {x_{B'}} + {x_{C'}}} \over 3} = {{ - 4 + 2 + 2} \over 3} = 0 \hfill \cr
{y_{G'}} = {{{y_{A'}} + {y_{B'}} + y{}_{C'}} \over 3} = {{1 + 4 - 2} \over 3} = 1 \hfill \cr} \right.\)
Vậy \(G'(0; 1)\) (**)
Từ (*) và (**) ta thấy \(G \equiv G'\)
Vậy trọng tâm tam giác \(ABC\) và \(A'B'C'\) trùng nhau.
+) \(I\) là trung điểm của \(AB\) thì: \(\left\{ \begin{array}{l}
{x_I} = \frac{{{x_A} + {x_B}}}{2}\\
{y_I} = \frac{{{y_A} + {y_B}}}{2}
\end{array} \right..\)
+) \(G\) là trọng tâm tam giác \(ABC\) thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right..\)
Lời giải chi tiết
Giả sử \(A({x_A};{y_A}), B({x_B};{y_B}), C({x_C};{y_C})\)
\(A'\) là trung điểm BC \(\Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = \frac{{{x_B} + {x_C}}}{2}\\{y_{A'}} = \frac{{{y_B} + {y_C}}}{2}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l} - 4 = \frac{{{x_B} + {x_C}}}{2}\\1 = \frac{{{y_B} + {y_C}}}{2}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = - 8 \left( 1 \right)\\{y_B} + {y_C} = 2 \left(2 \right)\end{array} \right.\)
\(B'\) là trung điểm CA \(\Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = \frac{{{x_C} + {x_A}}}{2}\\{y_{B'}} = \frac{{{y_C} + {y_A}}}{2}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}2 = \frac{{{x_C} + {x_A}}}{2}\\4 = \frac{{{y_C} + {y_A}}}{2}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_C} + {x_A} = 4 \left( 3 \right)\\{y_C} + {y_A} = 8 \left(4 \right)\end{array} \right.\)
\(C'\) là trung điểm AB \(\Leftrightarrow \left\{ \begin{array}{l}{x_{C'}} = \frac{{{x_A} + {x_B}}}{2}\\{y_{C'}} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}2 = \frac{{{x_A} + {x_B}}}{2}\\ - 2 = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 4 \left( 5 \right)\\{y_A} + {y_B} = - 4 \left(6 \right)\end{array} \right.\)
Từ (1), (3) và (5) ta có hệ:
\(\left\{ \begin{array}{l}{x_B} + {x_C} = - 8\\{x_C} + {x_A} = 4\\{x_A} + {x_B} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = - 8 - {x_B}\\ - 8 - {x_B} + {x_A} = 4\\{x_A} + {x_B} = 4\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{x_C} = - 8 - {x_B}\\{x_A} - {x_B} = 12\\{x_A} + {x_B} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 8\\{x_B} = - 4\\{x_C} = - 4\end{array} \right.\)
Từ (2), (4) và (6) ta có hệ:
\(\left\{ \begin{array}{l}{y_B} + {y_C} = 2\\{y_C} + {y_A} = 8\\{y_A} + {y_B} = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_C} = 2 - {y_B}\\2 - {y_B} + {y_A} = 8\\{y_A} + {y_B} = - 4\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}{y_C} = 2 - {y_B}\\{y_A} - {y_B} = 6\\{y_A} + {y_B} = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 1\\{y_B} = - 5\\{y_C} = 7\end{array} \right.\)
Vậy \(A\left( {8; 1} \right), B\left({ - 4; - 5} \right), C\left({ - 4; 7} \right)\).
Gọi \(G({x_G}; y{}_G)\) là trọng tâm của tam giác \(ABC\)
Khi đó ta có:
\(\left\{ \matrix{
{x_G} = {{{x_A} + {x_B} + {x_C}} \over 3} = {{8 - 4 - 4} \over 3} = 0 \hfill \cr
{y_G} = {{{y_A} + {y_B} + y{}_C} \over 3} = {{1 - 5 + 7} \over 3} = {1} \hfill \cr} \right.\)
Vậy \(G(0; 1)\) (*)
Gọi \(G'({x_{G'}}; y{}_{G'})\) là trọng tâm của tam giác \(A'B'C'\)
Khi đó ta có:
\(\left\{ \matrix{
{x_{G'}} = {{{x_{A'}} + {x_{B'}} + {x_{C'}}} \over 3} = {{ - 4 + 2 + 2} \over 3} = 0 \hfill \cr
{y_{G'}} = {{{y_{A'}} + {y_{B'}} + y{}_{C'}} \over 3} = {{1 + 4 - 2} \over 3} = 1 \hfill \cr} \right.\)
Vậy \(G'(0; 1)\) (**)
Từ (*) và (**) ta thấy \(G \equiv G'\)
Vậy trọng tâm tam giác \(ABC\) và \(A'B'C'\) trùng nhau.