Câu hỏi:
Phương pháp giải:
Sử dụng định lí dấu của tam thức bậc hai: “Tam thức bậc hai có hai nghiệm phân biệt thì rong khoảng hai nghiệm trái dấu với \(a\), ngoài khoảng hai nghiệm cùng dấu với \(a\)”.
Lời giải chi tiết:
\(\begin{array}{l}f\left( x \right) = 2x\left({x + 2} \right) - \left({x + 2} \right)\left({x + 1} \right)\\ = 2{x^2} + 4x - \left({{x^2} + 3x + 2} \right)\\ = {x^2} + x - 2\end{array}\)
Tam thức bậc hai \(f\left( x \right) = {x^2} + x - 2\) có \(a = 1 > 0\) và hai nghiệm \({x_1} = 1,{x_2} = - 2\) nên:
+) \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 2\end{array} \right.\)
+) \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
+) \(f\left( x \right) < 0 \Leftrightarrow - 2 < x < 1\).
Cách khác:
\(\begin{array}{l}
f\left(x \right) = 2x\left({x + 2} \right) - \left({x + 2} \right)\left({x + 1} \right)\\
= \left({x + 2} \right)\left({2x - x - 1} \right) \\= \left({x + 2} \right)\left({x - 1} \right).
\end{array}\)
Khi đó:
\(\begin{array}{l}
f\left(x \right) \ge 0 \Leftrightarrow \left({x + 2} \right)\left({x - 1} \right) \ge 0\\
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x + 2 \ge 0\\
x - 1 \ge 0
\end{array} \right.\\
\left\{ \begin{array}{l}
x + 2 \le 0\\
x - 1 \le 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \ge - 2\\
x \ge 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x \le - 2\\
x \le 1
\end{array} \right.
\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}
x \ge 1\\
x \le - 2
\end{array} \right..
\end{array}\)
\(\begin{array}{l}
f\left(x \right) < 0 \Leftrightarrow \left({x + 2} \right)\left({x - 1} \right) < 0\\
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x + 2 > 0\\
x - 1 < 0
\end{array} \right.\\
\left\{ \begin{array}{l}
x + 2 < 0\\
x - 1 > 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x > - 2\\
x < 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x < - 2\\
x > 1
\end{array} \right.
\end{array} \right.\\ \Leftrightarrow - 2 < x < 1.
\end{array}\)
Vậy \(f\left( x \right) > 0\) khi \(x \in \left( {-\infty; - 2} \right) \cup \left({1; + \infty } \right).\)
\(f(x) < 0\) khi \(x \in \left( { - 2; 1} \right).\)
\(f(x)=0\) khi \(x=-2\) hoặc \(x=1\).
\(y = 2x(x+2) (C_1)\) và \(y = (x+2)(x+1) (C_2).\)
Tính tọa độ các giao điểm \(A\) và \(B\) của \((C_1)\) và \((C_2)\)
Lời giải chi tiết:
*) Hàm số: \(y = 2x\left( {x + 2} \right) = 2{x^2} + 4x.\)
+) Tập xác định: R.
\(\begin{array}{l}
- \dfrac{b}{{2a}} = - \dfrac{4}{{2.2}} = - 1\\
- \dfrac{\Delta }{{4a}} = - 2
\end{array}\)
Hàm số có \(a = 2 > 0\) nên đồng biến trên \(\left( { - 1; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - 1} \right)\).
Ta có bảng biến thiên:
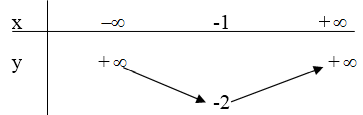
Đồ thị:
+) Giao điểm của đồ thị hàm số với các trục tọa độ: \(\left( { - 2; 0} \right), \left({0; 0} \right).\)
+) Trục đối xứng \(x=-1\)
+) Đỉnh: \(\left( { - 1; - 2} \right).\)
*) Xét hàm số \(y = \left( {x + 2} \right)\left({x + 1} \right) = {x^2} + 3x + 2.\)
\(\begin{array}{l}
- \dfrac{b}{{2a}} = - \dfrac{3}{{2.1}} = - \dfrac{3}{2}\\
- \dfrac{\Delta }{{4a}} = - \dfrac{1}{4}
\end{array}\)
Hàm số có \(a = 1 > 0\) nên đồng biến trên \(\left( { - \dfrac{3}{2}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \dfrac{3}{2}} \right)\)
Bảng biến thiên
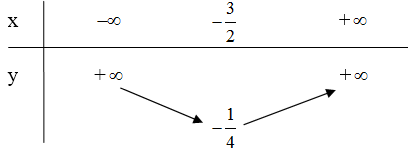
Đồ thị:
+) Giao điểm của đồ thị hàm số với các trục tọa độ: \(\left( { - 2; 0} \right), \left({-1; 0} \right).\)
+) Trục đối xứng \(x = - \dfrac{3}{2}\)
+) Đỉnh: \(\left( { - \dfrac{3}{2}; - \dfrac{1}{4}} \right)\)
Đồ thị (C1) và (C2)
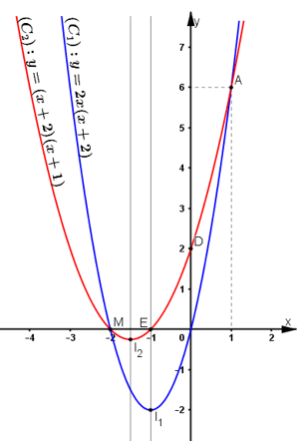
Hoành độ các giao điểm \(A\) và \(B\) của (C1) và (C2) là nghiệm của phương trình
Quan sát đồ thị ta thấy hai giao điểm \(A(-2; 0) , B(1; 6)\).
Cách khác:
\(\begin{array}{l}
2x\left({x + 2} \right) = \left({x + 2} \right)\left({x + 1} \right)\\
\Leftrightarrow 2x\left({x + 2} \right) - \left({x + 2} \right)\left({x + 1} \right) = 0\\
\Leftrightarrow \left({x + 2} \right)\left({2x - x - 1} \right) = 0\\
\Leftrightarrow \left({x + 2} \right)\left({x - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x + 2 = 0\\
x - 1 = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = - 2 \Rightarrow y = 0\\
x = 1 \Rightarrow y = 6
\end{array} \right.\\
\Rightarrow A\left({ - 2; 0} \right), B\left({1; 6} \right)
\end{array}\)
Lời giải chi tiết:
Theo đề bài ta có đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua A và B nên:
\(\left\{ \begin{array}{l}4x - 2b + c = 0\\a + b + c = 6\end{array} \right.\)
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
3a - 3b = - 6\\
c = 6 - \left({a + b} \right)
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a - b = - 2\\
c = 6 - \left({a + b} \right)
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a = b - 2\\
c = 6 - \left({b - 2 + b} \right)
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a = b - 2\\
c = 8 - 2b
\end{array} \right.
\end{array}\)
Để hàm số \(y = a{x^2} + bx + c\) đạt giá trị lớn nhất bằng 8 thì:
\(\left\{ \begin{array}{l}a < 0\\\dfrac{{ - \Delta }}{{4a}} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\dfrac{{4ac - {b^2}}}{{4a}} = 8\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a < 0\\4ac - {b^2} = 32a \left( 2 \right)\end{array} \right.\)
Thay (1) vào (2) ta có:
$4(b-2)(8-2 b)-b^{2}=32(b-2)$
$\Leftrightarrow 4\left(8 b-2 b^{2}-16+4 b\right)-b^{2}=32 b-64$
$\Leftrightarrow 32 b-8 b^{2}-64+16 b-b^{2}=32 b-64$
$\Leftrightarrow 9 b^{2}-16 b=0$.
$\Leftrightarrow 9 b(9 b-16)=0$
$\Leftrightarrow\left[\begin{array}{l}9 b=0 \\ 9 b-16=0\end{array} \Leftrightarrow\left[\begin{array}{l}b=0 \\ b=\frac{16}{9}\end{array}\right.\right.$
+) Với \(b = 0\) ta có: \(a = - 2, c = 8 \Rightarrow y = - 2{x^2} + 8.\)
+) Với \(b = \dfrac{{16}}{9}\) thì \(a = - \dfrac{2}{9}, c = \dfrac{{40}}{9}\)\(\Rightarrow y = - \dfrac{2}{9}{x^2} + \dfrac{{16}}{9}x + \dfrac{{40}}{9}.\)
Câu a
Xét dấu biểu thức: \(f(x) = 2x(x+2) – (x+2)(x+1).\)Phương pháp giải:
Sử dụng định lí dấu của tam thức bậc hai: “Tam thức bậc hai có hai nghiệm phân biệt thì rong khoảng hai nghiệm trái dấu với \(a\), ngoài khoảng hai nghiệm cùng dấu với \(a\)”.
Lời giải chi tiết:
\(\begin{array}{l}f\left( x \right) = 2x\left({x + 2} \right) - \left({x + 2} \right)\left({x + 1} \right)\\ = 2{x^2} + 4x - \left({{x^2} + 3x + 2} \right)\\ = {x^2} + x - 2\end{array}\)
Tam thức bậc hai \(f\left( x \right) = {x^2} + x - 2\) có \(a = 1 > 0\) và hai nghiệm \({x_1} = 1,{x_2} = - 2\) nên:
+) \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 2\end{array} \right.\)
+) \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
+) \(f\left( x \right) < 0 \Leftrightarrow - 2 < x < 1\).
Cách khác:
\(\begin{array}{l}
f\left(x \right) = 2x\left({x + 2} \right) - \left({x + 2} \right)\left({x + 1} \right)\\
= \left({x + 2} \right)\left({2x - x - 1} \right) \\= \left({x + 2} \right)\left({x - 1} \right).
\end{array}\)
Khi đó:
\(\begin{array}{l}
f\left(x \right) \ge 0 \Leftrightarrow \left({x + 2} \right)\left({x - 1} \right) \ge 0\\
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x + 2 \ge 0\\
x - 1 \ge 0
\end{array} \right.\\
\left\{ \begin{array}{l}
x + 2 \le 0\\
x - 1 \le 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \ge - 2\\
x \ge 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x \le - 2\\
x \le 1
\end{array} \right.
\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}
x \ge 1\\
x \le - 2
\end{array} \right..
\end{array}\)
\(\begin{array}{l}
f\left(x \right) < 0 \Leftrightarrow \left({x + 2} \right)\left({x - 1} \right) < 0\\
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x + 2 > 0\\
x - 1 < 0
\end{array} \right.\\
\left\{ \begin{array}{l}
x + 2 < 0\\
x - 1 > 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x > - 2\\
x < 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x < - 2\\
x > 1
\end{array} \right.
\end{array} \right.\\ \Leftrightarrow - 2 < x < 1.
\end{array}\)
Vậy \(f\left( x \right) > 0\) khi \(x \in \left( {-\infty; - 2} \right) \cup \left({1; + \infty } \right).\)
\(f(x) < 0\) khi \(x \in \left( { - 2; 1} \right).\)
\(f(x)=0\) khi \(x=-2\) hoặc \(x=1\).
Câu b
Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc các đồ thị của các hàm số sau\(y = 2x(x+2) (C_1)\) và \(y = (x+2)(x+1) (C_2).\)
Tính tọa độ các giao điểm \(A\) và \(B\) của \((C_1)\) và \((C_2)\)
Lời giải chi tiết:
*) Hàm số: \(y = 2x\left( {x + 2} \right) = 2{x^2} + 4x.\)
+) Tập xác định: R.
\(\begin{array}{l}
- \dfrac{b}{{2a}} = - \dfrac{4}{{2.2}} = - 1\\
- \dfrac{\Delta }{{4a}} = - 2
\end{array}\)
Hàm số có \(a = 2 > 0\) nên đồng biến trên \(\left( { - 1; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - 1} \right)\).
Ta có bảng biến thiên:

Đồ thị:
+) Giao điểm của đồ thị hàm số với các trục tọa độ: \(\left( { - 2; 0} \right), \left({0; 0} \right).\)
+) Trục đối xứng \(x=-1\)
+) Đỉnh: \(\left( { - 1; - 2} \right).\)
*) Xét hàm số \(y = \left( {x + 2} \right)\left({x + 1} \right) = {x^2} + 3x + 2.\)
\(\begin{array}{l}
- \dfrac{b}{{2a}} = - \dfrac{3}{{2.1}} = - \dfrac{3}{2}\\
- \dfrac{\Delta }{{4a}} = - \dfrac{1}{4}
\end{array}\)
Hàm số có \(a = 1 > 0\) nên đồng biến trên \(\left( { - \dfrac{3}{2}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \dfrac{3}{2}} \right)\)
Bảng biến thiên

Đồ thị:
+) Giao điểm của đồ thị hàm số với các trục tọa độ: \(\left( { - 2; 0} \right), \left({-1; 0} \right).\)
+) Trục đối xứng \(x = - \dfrac{3}{2}\)
+) Đỉnh: \(\left( { - \dfrac{3}{2}; - \dfrac{1}{4}} \right)\)
Đồ thị (C1) và (C2)

Hoành độ các giao điểm \(A\) và \(B\) của (C1) và (C2) là nghiệm của phương trình
Quan sát đồ thị ta thấy hai giao điểm \(A(-2; 0) , B(1; 6)\).
Cách khác:
\(\begin{array}{l}
2x\left({x + 2} \right) = \left({x + 2} \right)\left({x + 1} \right)\\
\Leftrightarrow 2x\left({x + 2} \right) - \left({x + 2} \right)\left({x + 1} \right) = 0\\
\Leftrightarrow \left({x + 2} \right)\left({2x - x - 1} \right) = 0\\
\Leftrightarrow \left({x + 2} \right)\left({x - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x + 2 = 0\\
x - 1 = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = - 2 \Rightarrow y = 0\\
x = 1 \Rightarrow y = 6
\end{array} \right.\\
\Rightarrow A\left({ - 2; 0} \right), B\left({1; 6} \right)
\end{array}\)
Câu c
Tính các hệ số \(a, b, c\) để hàm số \(y = ax^2+ bx + c\) có giá trị lớn nhất bằng \(8\) và đồ thị của nó đi qua \(A\) và \(B\).Lời giải chi tiết:
Theo đề bài ta có đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua A và B nên:
\(\left\{ \begin{array}{l}4x - 2b + c = 0\\a + b + c = 6\end{array} \right.\)
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
3a - 3b = - 6\\
c = 6 - \left({a + b} \right)
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a - b = - 2\\
c = 6 - \left({a + b} \right)
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a = b - 2\\
c = 6 - \left({b - 2 + b} \right)
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a = b - 2\\
c = 8 - 2b
\end{array} \right.
\end{array}\)
Để hàm số \(y = a{x^2} + bx + c\) đạt giá trị lớn nhất bằng 8 thì:
\(\left\{ \begin{array}{l}a < 0\\\dfrac{{ - \Delta }}{{4a}} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\dfrac{{4ac - {b^2}}}{{4a}} = 8\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a < 0\\4ac - {b^2} = 32a \left( 2 \right)\end{array} \right.\)
Thay (1) vào (2) ta có:
$4(b-2)(8-2 b)-b^{2}=32(b-2)$
$\Leftrightarrow 4\left(8 b-2 b^{2}-16+4 b\right)-b^{2}=32 b-64$
$\Leftrightarrow 32 b-8 b^{2}-64+16 b-b^{2}=32 b-64$
$\Leftrightarrow 9 b^{2}-16 b=0$.
$\Leftrightarrow 9 b(9 b-16)=0$
$\Leftrightarrow\left[\begin{array}{l}9 b=0 \\ 9 b-16=0\end{array} \Leftrightarrow\left[\begin{array}{l}b=0 \\ b=\frac{16}{9}\end{array}\right.\right.$
+) Với \(b = 0\) ta có: \(a = - 2, c = 8 \Rightarrow y = - 2{x^2} + 8.\)
+) Với \(b = \dfrac{{16}}{9}\) thì \(a = - \dfrac{2}{9}, c = \dfrac{{40}}{9}\)\(\Rightarrow y = - \dfrac{2}{9}{x^2} + \dfrac{{16}}{9}x + \dfrac{{40}}{9}.\)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!