Câu hỏi: Tính:
Phương pháp giải:
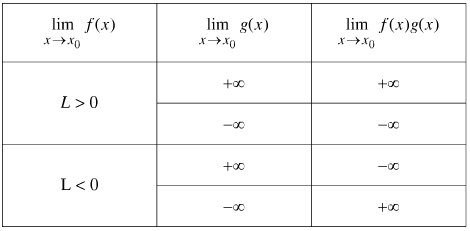
Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \left({{x^4} - {x^2} + x - 1} \right) \\= \mathop {\lim }\limits_{x \to + \infty } {x^4}\left({1 - \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^3}}} - \dfrac{1}{{{x^4}}}} \right)\\
\mathop {\lim }\limits_{x \to + \infty } {x^4} = + \infty \\
\mathop {\lim }\limits_{x \to + \infty } \left({1 - \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^3}}} - \dfrac{1}{{{x^4}}}} \right) = 1 > 0\\
\Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left({{x^4} - {x^2} + x - 1} \right) = + \infty \\
\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left({ - 2{x^3} + 3{x^2} - 5} \right) \\= \mathop {\lim }\limits_{x \to - \infty } {x^3}\left({ - 2 + \dfrac{3}{x} - \dfrac{5}{{{x^2}}}} \right)\\
\mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty \\
\mathop {\lim }\limits_{x \to - \infty } \left({ - 2 + \dfrac{3}{x} - \dfrac{5}{{{x^2}}}} \right) = - 2 < 0\\
\Rightarrow \mathop {\lim }\limits_{x \to - \infty } {x^3}\left({ - 2 + \dfrac{3}{x} - \dfrac{5}{{{x^2}}}} \right) = + \infty \\
\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left({\sqrt {{x^2} - 2x + 5} } \right) \\ = \mathop {\lim }\limits_{x \to - \infty } \sqrt {{x^2}\left({1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \right)} \\= \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {1 - \dfrac{2}{x} + \dfrac{5}{{{x^2}}}} \\
= \mathop {\lim }\limits_{x \to - \infty } \left[ { - x\sqrt {1 - \dfrac{2}{x} + \dfrac{5}{{{x^2}}}} } \right]\\
\mathop {\lim }\limits_{x \to - \infty } \left({ - x} \right) = + \infty \\
\mathop {\lim }\limits_{x \to - \infty } \left({\sqrt {1 - \dfrac{2}{x} + \dfrac{5}{{{x^2}}}} } \right) = 1 > 0\\
\Rightarrow \mathop {\lim }\limits_{x \to - \infty } \left({\sqrt {{x^2} - 2x + 5} } \right) = + \infty \\
\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {{x^2} + 1} + x}}{{5 - 2x}} \\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {{x^2}\left({1 + \dfrac{1}{{{x^2}}}} \right)} + x}}{{5 - 2x}} \\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\left| x \right|\sqrt {1 + \dfrac{1}{{{x^2}}}} + x}}{{5 - 2x}} \\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x\sqrt {1 + \dfrac{1}{{{x^2}}}} + x}}{{5 - 2x}}\\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x\left({\sqrt {1 + \dfrac{1}{{{x^2}}}} + 1} \right)}}{x\left({\dfrac{5}{x} - 2} \right)}\\
= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {1 + \dfrac{1}{{{x^2}}}} + 1}}{{\dfrac{5}{x} - 2}} \\= \dfrac{{1 + 1}}{{ - 2}} = - 1
\end{array}\)
Câu a
\(\eqalign{& \mathop {\lim }\limits_{x \to + \infty } ({x^4} - {x^2} + x - 1) \cr} \)Phương pháp giải:

Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \left({{x^4} - {x^2} + x - 1} \right) \\= \mathop {\lim }\limits_{x \to + \infty } {x^4}\left({1 - \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^3}}} - \dfrac{1}{{{x^4}}}} \right)\\
\mathop {\lim }\limits_{x \to + \infty } {x^4} = + \infty \\
\mathop {\lim }\limits_{x \to + \infty } \left({1 - \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^3}}} - \dfrac{1}{{{x^4}}}} \right) = 1 > 0\\
\Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left({{x^4} - {x^2} + x - 1} \right) = + \infty \\
\end{array}\)
Câu b
\(\eqalign{& & \mathop {\lim }\limits_{x \to - \infty } ( - 2{x^3} + 3{x^2} - 5) \cr }\)Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left({ - 2{x^3} + 3{x^2} - 5} \right) \\= \mathop {\lim }\limits_{x \to - \infty } {x^3}\left({ - 2 + \dfrac{3}{x} - \dfrac{5}{{{x^2}}}} \right)\\
\mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty \\
\mathop {\lim }\limits_{x \to - \infty } \left({ - 2 + \dfrac{3}{x} - \dfrac{5}{{{x^2}}}} \right) = - 2 < 0\\
\Rightarrow \mathop {\lim }\limits_{x \to - \infty } {x^3}\left({ - 2 + \dfrac{3}{x} - \dfrac{5}{{{x^2}}}} \right) = + \infty \\
\end{array}\)
Câu c
\(\eqalign{&\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr } \)Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left({\sqrt {{x^2} - 2x + 5} } \right) \\ = \mathop {\lim }\limits_{x \to - \infty } \sqrt {{x^2}\left({1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \right)} \\= \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {1 - \dfrac{2}{x} + \dfrac{5}{{{x^2}}}} \\
= \mathop {\lim }\limits_{x \to - \infty } \left[ { - x\sqrt {1 - \dfrac{2}{x} + \dfrac{5}{{{x^2}}}} } \right]\\
\mathop {\lim }\limits_{x \to - \infty } \left({ - x} \right) = + \infty \\
\mathop {\lim }\limits_{x \to - \infty } \left({\sqrt {1 - \dfrac{2}{x} + \dfrac{5}{{{x^2}}}} } \right) = 1 > 0\\
\Rightarrow \mathop {\lim }\limits_{x \to - \infty } \left({\sqrt {{x^2} - 2x + 5} } \right) = + \infty \\
\end{array}\)
Câu d
\(\eqalign{&\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr} \)Lời giải chi tiết:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {{x^2} + 1} + x}}{{5 - 2x}} \\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {{x^2}\left({1 + \dfrac{1}{{{x^2}}}} \right)} + x}}{{5 - 2x}} \\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\left| x \right|\sqrt {1 + \dfrac{1}{{{x^2}}}} + x}}{{5 - 2x}} \\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x\sqrt {1 + \dfrac{1}{{{x^2}}}} + x}}{{5 - 2x}}\\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x\left({\sqrt {1 + \dfrac{1}{{{x^2}}}} + 1} \right)}}{x\left({\dfrac{5}{x} - 2} \right)}\\
= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\sqrt {1 + \dfrac{1}{{{x^2}}}} + 1}}{{\dfrac{5}{x} - 2}} \\= \dfrac{{1 + 1}}{{ - 2}} = - 1
\end{array}\)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!