Câu hỏi: Cho tam giác \(ABC\) đều cạnh \(a\). Tính độ dài của các vectơ \(\overrightarrow{AB}+ \overrightarrow{BC}\) và \(\overrightarrow{AB}- \overrightarrow{BC}.\)
Phương pháp giải
Với quy tắc ba điểm tùy ý \(A, B, C\) ta luôn có:
\(+) \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\(+) \overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (quy tắc trừ).
Lời giải chi tiết
Ta có \(\overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}\)
\(\left | \overrightarrow{AB}+\overrightarrow{BC} \right | = \left | \overrightarrow{AC} \right |= a.\)
Ta có: \(\overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{AB} +\overrightarrow{CB}.\)
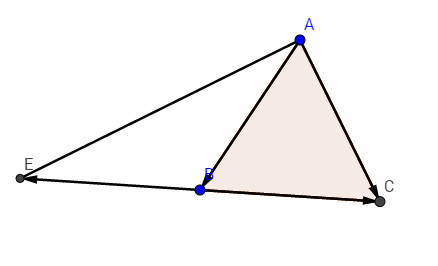
Trên tia \(CB,\) ta dựng \(\overrightarrow{BE} = \overrightarrow{CB}.\)
\(\Rightarrow \overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow {AB} + \overrightarrow {CB} \) \( = \overrightarrow{AB} +\overrightarrow{BE}= \overrightarrow{AE}\)
Tam giác \(EAC\) có đường trung tuyến \(AB\) bằng nửa cạnh \(CE\) nên là tam giác vuông tại \(A\)
Mà \(AC = a, CE = 2a,\) nên theo định lý Pitago ta có:
\(A{E^2} + A{C^2} = C{E^2} \) \( \Leftrightarrow AE = \sqrt {C{E^2} - A{C^2}} \)
\(= \sqrt {4{a^2} - {a^2}} \)\(= a\sqrt 3. \)
Vậy \(\left | \overrightarrow{AB } -\overrightarrow{BC}\right | = \left | \overrightarrow{AE} \right | = a\sqrt3.\)
Cách khác:
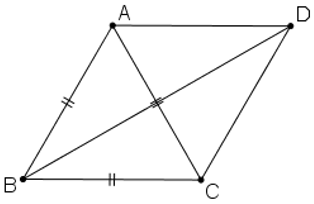
Dựng hình bình hành ABCD ta có:
\(\begin{array}{l}\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {AB} + \overrightarrow {CB} \\ = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AB} \\ = \overrightarrow {DB} \\ \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {BC} } \right| = \left| {\overrightarrow {DB} } \right| = DB\end{array}\)
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
$\mathrm{AO}=\frac{\mathrm{AC}}{2}=\frac{\mathrm{a}}{2}$
$\Rightarrow \mathrm{BO}=\sqrt{\mathrm{AB}^{2}-\mathrm{AO}^{2}}=\sqrt{\mathrm{a}^{2}-\left(\frac{\mathrm{a}}{2}\right)^{2}}=\frac{\mathrm{a} \sqrt{3}}{2}$
$\Rightarrow \mathrm{BD}=2 \mathrm{BO}=\mathrm{a} \sqrt{3}$
Vậy $|\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{BC}}|=\mathrm{a} \sqrt{3}$
Với quy tắc ba điểm tùy ý \(A, B, C\) ta luôn có:
\(+) \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (quy tắc ba điểm).
\(+) \overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \) (quy tắc trừ).
Lời giải chi tiết
Ta có \(\overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}\)
\(\left | \overrightarrow{AB}+\overrightarrow{BC} \right | = \left | \overrightarrow{AC} \right |= a.\)
Ta có: \(\overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{AB} +\overrightarrow{CB}.\)
Trên tia \(CB,\) ta dựng \(\overrightarrow{BE} = \overrightarrow{CB}.\)
\(\Rightarrow \overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow {AB} + \overrightarrow {CB} \) \( = \overrightarrow{AB} +\overrightarrow{BE}= \overrightarrow{AE}\)
Tam giác \(EAC\) có đường trung tuyến \(AB\) bằng nửa cạnh \(CE\) nên là tam giác vuông tại \(A\)
Mà \(AC = a, CE = 2a,\) nên theo định lý Pitago ta có:
\(A{E^2} + A{C^2} = C{E^2} \) \( \Leftrightarrow AE = \sqrt {C{E^2} - A{C^2}} \)
\(= \sqrt {4{a^2} - {a^2}} \)\(= a\sqrt 3. \)
Vậy \(\left | \overrightarrow{AB } -\overrightarrow{BC}\right | = \left | \overrightarrow{AE} \right | = a\sqrt3.\)
Cách khác:
Dựng hình bình hành ABCD ta có:
\(\begin{array}{l}\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {AB} + \overrightarrow {CB} \\ = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AB} \\ = \overrightarrow {DB} \\ \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {BC} } \right| = \left| {\overrightarrow {DB} } \right| = DB\end{array}\)
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
$\mathrm{AO}=\frac{\mathrm{AC}}{2}=\frac{\mathrm{a}}{2}$
$\Rightarrow \mathrm{BO}=\sqrt{\mathrm{AB}^{2}-\mathrm{AO}^{2}}=\sqrt{\mathrm{a}^{2}-\left(\frac{\mathrm{a}}{2}\right)^{2}}=\frac{\mathrm{a} \sqrt{3}}{2}$
$\Rightarrow \mathrm{BD}=2 \mathrm{BO}=\mathrm{a} \sqrt{3}$
Vậy $|\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{BC}}|=\mathrm{a} \sqrt{3}$