Câu hỏi: Cho tứ diện đều \(ABCD\). Gọi \((H)\) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số \(\dfrac{{{V_{(H)}}}}{{{V_{ABCD}}}}\).
Phương pháp giải
- Tính thể tích khối tứ diện đều.
- Tính thể tích khối bát diện đều.
- Từ đó suy ra tỉ số.
Lời giải chi tiết
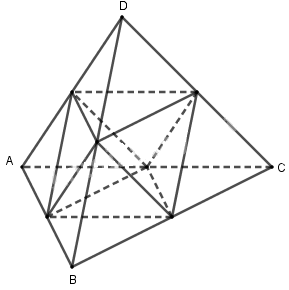
Gọi cạnh của tứ diện đều là \(a\) thì cạnh của hình bát diện đều \(\left( H \right)\) là \(\dfrac{a}{2}\).
+) Tính thể tích tứ diện đều \(ABCD\) cạnh \(a\).
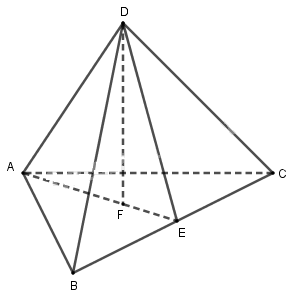
Gọi \(E\) là trung điểm của \(BC\) và \(F\) là trọng tâm của tam giác \(ABC\).
Khi đó \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\) và \(DF = \sqrt {D{A^2} - A{F^2}} \) \(= \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
\(\Rightarrow {V_{ABCD}} = \dfrac{1}{3}{S_{ABC}}. DF\)\(= \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
+) Tính thể tích khối bát diện đều cạnh \(\dfrac{a}{2}\).
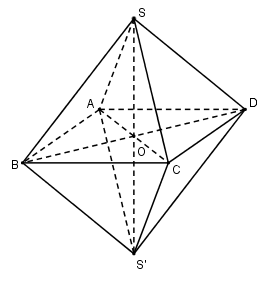
Xét bát diện đều \(SABCDS'\) có cạnh \(\dfrac{a}{2}\).
Thể tích khối bát diện đều \({V_{\left( H \right)}} = 2{V_{S. ABCD}}\)
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)
Vì \(ABCD\) là hình vuông nên \(AC = BD = \dfrac{{a\sqrt 2 }}{2}\)\(\Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{4}\)
\(SO \bot \left( {ABCD} \right)\)\(\Rightarrow SO \bot OA\) \(\Rightarrow \Delta SOA\) vuông tại \(O\)
\(\Rightarrow SO = \sqrt {S{A^2} - O{A^2}} \)\(= \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} - {{\left({\dfrac{{a\sqrt 2 }}{4}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{4}\)
\(\Rightarrow {V_{S. ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\)\(= \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{4}.{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{{a^3}\sqrt 2 }}{{48}}\)
\(\Rightarrow {V_{\left( H \right)}} = 2.\dfrac{{{a^3}\sqrt 2 }}{{48}} = \dfrac{{{a^3}\sqrt 2 }}{{24}}\)
Vậy \(\dfrac{{{V_{(H)}}}}{{{V_{ABCD}}}} = \dfrac{1}{2}\).
- Tính thể tích khối tứ diện đều.
- Tính thể tích khối bát diện đều.
- Từ đó suy ra tỉ số.
Lời giải chi tiết
Gọi cạnh của tứ diện đều là \(a\) thì cạnh của hình bát diện đều \(\left( H \right)\) là \(\dfrac{a}{2}\).
+) Tính thể tích tứ diện đều \(ABCD\) cạnh \(a\).
Gọi \(E\) là trung điểm của \(BC\) và \(F\) là trọng tâm của tam giác \(ABC\).
Khi đó \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\) và \(DF = \sqrt {D{A^2} - A{F^2}} \) \(= \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
\(\Rightarrow {V_{ABCD}} = \dfrac{1}{3}{S_{ABC}}. DF\)\(= \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
+) Tính thể tích khối bát diện đều cạnh \(\dfrac{a}{2}\).
Xét bát diện đều \(SABCDS'\) có cạnh \(\dfrac{a}{2}\).
Thể tích khối bát diện đều \({V_{\left( H \right)}} = 2{V_{S. ABCD}}\)
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)
Vì \(ABCD\) là hình vuông nên \(AC = BD = \dfrac{{a\sqrt 2 }}{2}\)\(\Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{4}\)
\(SO \bot \left( {ABCD} \right)\)\(\Rightarrow SO \bot OA\) \(\Rightarrow \Delta SOA\) vuông tại \(O\)
\(\Rightarrow SO = \sqrt {S{A^2} - O{A^2}} \)\(= \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} - {{\left({\dfrac{{a\sqrt 2 }}{4}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{4}\)
\(\Rightarrow {V_{S. ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\)\(= \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{4}.{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{{a^3}\sqrt 2 }}{{48}}\)
\(\Rightarrow {V_{\left( H \right)}} = 2.\dfrac{{{a^3}\sqrt 2 }}{{48}} = \dfrac{{{a^3}\sqrt 2 }}{{24}}\)
Vậy \(\dfrac{{{V_{(H)}}}}{{{V_{ABCD}}}} = \dfrac{1}{2}\).