Câu hỏi: Xét hai số phức $z_1, z_2$ thỏa mãn $2\left|\bar{z}_1+i\right|=\left|\bar{z}_1-z_1-2 i\right|$ và $\left|z_2-i-10\right|=1$. Giá trị nhỏ nhất của biểu thức $\left|z_1-z_2\right|$ bằng
A. $\sqrt{\sqrt{101}+1}$.
B. $3 \sqrt{5}-1$.
C. $\sqrt{10}+1$.
D. $\sqrt{\sqrt{101}-1}$.
A. $\sqrt{\sqrt{101}+1}$.
B. $3 \sqrt{5}-1$.
C. $\sqrt{10}+1$.
D. $\sqrt{\sqrt{101}-1}$.
Gọi $z_1=a+b i(a, b \in \mathbb{R})$.
Ta có $2\left|\bar{z}_1+i\right|=\left|\bar{z}_1-z_1-2 i\right| \Rightarrow b=\dfrac{a^2}{4}$.
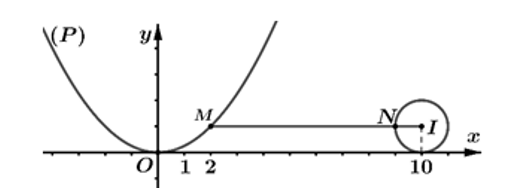
Tập hợp điểm $M$ biểu diễn $z_1$ là parabol $(P): y=\dfrac{1}{4} x^2$ có đỉnh $O(0 ; 0)$.
Ta có: $\left|z_2-i-10\right|=1 \Rightarrow$ Tập hợp điểm $N$ biễu diễn $z_2$ là đường tròn $(C)$ có tâm $I(10 ; 1), R=$ 1.
Khi đó $P=\left|z_1-z_2\right|=M N$ là khoảng cách từ một điểm thuộc $(P)$ đến một điểm thuộc $(C)$.
Ta có: $M N+N I \geq M I \Rightarrow M N \geq M I-N I=M I-1 \Rightarrow M N_{\min } \Leftrightarrow I M_{\min }$.
Mà $I M^2=(x-10)^2+\left(\dfrac{x^2}{4}-1\right)^2$
$=\left(\dfrac{x^2}{4}-4\right)^2+\dfrac{5}{2}(x-4)^2+45 \geq 45 \Rightarrow I M \geq \sqrt{45}=3 \sqrt{5}$
 Do đó $M N_{\min }=3 \sqrt{5}-1$.
Do đó $M N_{\min }=3 \sqrt{5}-1$.
Ta có $2\left|\bar{z}_1+i\right|=\left|\bar{z}_1-z_1-2 i\right| \Rightarrow b=\dfrac{a^2}{4}$.
Tập hợp điểm $M$ biểu diễn $z_1$ là parabol $(P): y=\dfrac{1}{4} x^2$ có đỉnh $O(0 ; 0)$.
Ta có: $\left|z_2-i-10\right|=1 \Rightarrow$ Tập hợp điểm $N$ biễu diễn $z_2$ là đường tròn $(C)$ có tâm $I(10 ; 1), R=$ 1.
Khi đó $P=\left|z_1-z_2\right|=M N$ là khoảng cách từ một điểm thuộc $(P)$ đến một điểm thuộc $(C)$.
Ta có: $M N+N I \geq M I \Rightarrow M N \geq M I-N I=M I-1 \Rightarrow M N_{\min } \Leftrightarrow I M_{\min }$.
Mà $I M^2=(x-10)^2+\left(\dfrac{x^2}{4}-1\right)^2$
$=\left(\dfrac{x^2}{4}-4\right)^2+\dfrac{5}{2}(x-4)^2+45 \geq 45 \Rightarrow I M \geq \sqrt{45}=3 \sqrt{5}$
Đáp án B.