Google
Câu hỏi: Cho số phức $z, z_1, z_2$ thỏa mãn $\left|z_1-4-5 i\right|=\left|z_2-1\right|=1$ và $|\bar{z}+4 i|=|z-8+4 i|$. Tính $\left|z_1-z_2\right|$ khi $P=\left|z-z_1\right|+\left|z-z_2\right|$ đạt giá trị nhỏ nhất.
A. $\sqrt{41}$.
B. 8 .
C. $2 \sqrt{5}$.
D. 6 .
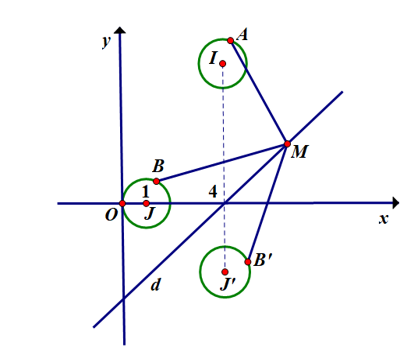Gọi $A$ là điểm biểu diễn của số phức $z_1$. Suy ra $A$ thuộc đường tròn $\left(C_1\right)$ tâm $I(4 ; 5), R=1$
Gọi $B$ là điểm biểu diễn của số phức $z_2$. Suy ra $B$ thuộc đường tròn $\left(C_2\right)$ tâm $J(1 ; 0), R=1$.
Gọi $M(x ; y)$ là điểm biểu diễn của số phức $z=x+y i$.
Theo giả thiết $|\bar{z}+4 i|=|z-8+4 i| \Leftrightarrow x-y=4$. Suy ra M thuộc đường thẳng $(d) x-y-4=$
0.
Gọi $\left(C_2{ }^{\prime}\right)$ có tâm $J^{\prime}(4 ;-3), R=1$ là đường tròn đối xứng với đường tròn $\left(C_2\right)$ tâm $J(1 ; 0), R_2=$ 1 qua đường thẳng $\mathrm{d}$.
Gọi $B^{\prime}$ là điểm đối xứng với đối xứng với $B$ qua đường thẳng $\mathrm{d}$.
Ta có $P=\left|z-z_1\right|+\left|z-z_2\right|=M A+M B=M A+M B^{\prime} \geq A B^{\prime} \geq I J^{\prime}-R_1-R_2=6$.
Dấu " = " xảy ra khi và chỉ khi các điểm $I, A, B^{\prime}, M, \mathrm{~J}^{\prime}$ theo thứ tự thẳng hàng. Khi đó $\overrightarrow{I A}=\dfrac{1}{8} \overrightarrow{I J^{\prime}}$ suy ra $A(4 ; 4)$ và $\overrightarrow{J B^{\prime}}=\dfrac{1}{8} \overrightarrow{J^{\prime} I}$ suy $\operatorname{ra} B^{\prime}(4 ;-2) \Rightarrow B(2 ; 0)$.
Ta có $A B=2 \sqrt{5}$. Vậy $\left|z_1-z_2\right|=2 \sqrt{5}$.
A. $\sqrt{41}$.
B. 8 .
C. $2 \sqrt{5}$.
D. 6 .
Gọi $B$ là điểm biểu diễn của số phức $z_2$. Suy ra $B$ thuộc đường tròn $\left(C_2\right)$ tâm $J(1 ; 0), R=1$.
Gọi $M(x ; y)$ là điểm biểu diễn của số phức $z=x+y i$.
Theo giả thiết $|\bar{z}+4 i|=|z-8+4 i| \Leftrightarrow x-y=4$. Suy ra M thuộc đường thẳng $(d) x-y-4=$
0.
Gọi $\left(C_2{ }^{\prime}\right)$ có tâm $J^{\prime}(4 ;-3), R=1$ là đường tròn đối xứng với đường tròn $\left(C_2\right)$ tâm $J(1 ; 0), R_2=$ 1 qua đường thẳng $\mathrm{d}$.
Gọi $B^{\prime}$ là điểm đối xứng với đối xứng với $B$ qua đường thẳng $\mathrm{d}$.
Ta có $P=\left|z-z_1\right|+\left|z-z_2\right|=M A+M B=M A+M B^{\prime} \geq A B^{\prime} \geq I J^{\prime}-R_1-R_2=6$.
Dấu " = " xảy ra khi và chỉ khi các điểm $I, A, B^{\prime}, M, \mathrm{~J}^{\prime}$ theo thứ tự thẳng hàng. Khi đó $\overrightarrow{I A}=\dfrac{1}{8} \overrightarrow{I J^{\prime}}$ suy ra $A(4 ; 4)$ và $\overrightarrow{J B^{\prime}}=\dfrac{1}{8} \overrightarrow{J^{\prime} I}$ suy $\operatorname{ra} B^{\prime}(4 ;-2) \Rightarrow B(2 ; 0)$.
Ta có $A B=2 \sqrt{5}$. Vậy $\left|z_1-z_2\right|=2 \sqrt{5}$.
Đáp án C.
