Google
Câu hỏi: Xét hai số phức $z_1, z_2$ thoả mãn $\left|z_1+2\right|+\left|z_1-1\right|+\left|z_1-\overline{z_1}-2\right|=5$ và $\left|i . z_2+3-2 i\right|=2$. Khi $\left|z_1-z_2\right|$ đạt giá trị lớn nhất thì $\left|i . z_1+z_2-1\right|$ bằng
A. $\dfrac{\sqrt{65}}{5}$.
B. $\dfrac{\sqrt{185}}{5}$.
C. $\dfrac{\sqrt{290}}{5}$.
D. $\dfrac{8 \sqrt{5}}{5}$.
A. $\dfrac{\sqrt{65}}{5}$.
B. $\dfrac{\sqrt{185}}{5}$.
C. $\dfrac{\sqrt{290}}{5}$.
D. $\dfrac{8 \sqrt{5}}{5}$.
Đặt ${{z}_{1}}=x+yi(x,y\in \mathbb{R})$.
Ta có
$\left| {{z}_{1}}+2 \right|+\left| {{z}_{1}}-1 \right|+\left| {{z}_{1}}-{{{\bar{z}}}_{1}}-2 \right|=5$ $\Leftrightarrow \sqrt{{{(x+2)}^{2}}+{{y}^{2}}}+\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}+\sqrt{4{{y}^{2}}+4}=5.(*)$
Nhận thấy
$\sqrt{{{(x+2)}^{2}}+{{y}^{2}}}+\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}+\sqrt{4{{y}^{2}}+4}=5$ $\Leftrightarrow \left\{ \begin{aligned}
& y=0 \\
& (x+2)(1-x)\ge 0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& y=0 \\
& -2\le x\le 1 \\
\end{aligned} \right.$
Vậy $M\left(z_1\right)$ thuộc đoạn $AB$ với $A(-2 ; 0), B(1 ; 0)$.
Mặt khác
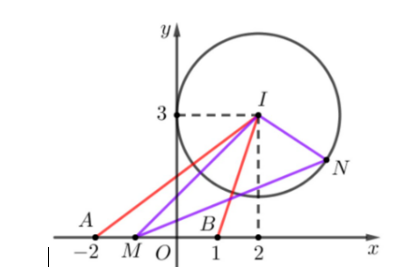Khi đó $\left|z_1-z_2\right|=M N \leq I M+I N=I M+R \leq \max \{I A, I B\}+R=\max \{5, \sqrt{10}\}+2=5+2=7$.
Dấu bằng xảy ra khi $M \equiv A(-2 ; 0) \Rightarrow z_1=-2$ và $M \equiv A, I, N$ thẳng hàng theo thứ tự tức là
Ta có
$\left| {{z}_{1}}+2 \right|+\left| {{z}_{1}}-1 \right|+\left| {{z}_{1}}-{{{\bar{z}}}_{1}}-2 \right|=5$ $\Leftrightarrow \sqrt{{{(x+2)}^{2}}+{{y}^{2}}}+\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}+\sqrt{4{{y}^{2}}+4}=5.(*)$
Nhận thấy
$V T_{(*)} \geq \sqrt{(x+2)^2}+\sqrt{(x-1)^2}+\sqrt{4}=|x+2|+|1-x|+2 \geq|(x+2)+(1-x)|+2=5=V P_{(*)}$.
nên$\sqrt{{{(x+2)}^{2}}+{{y}^{2}}}+\sqrt{{{(x-1)}^{2}}+{{y}^{2}}}+\sqrt{4{{y}^{2}}+4}=5$ $\Leftrightarrow \left\{ \begin{aligned}
& y=0 \\
& (x+2)(1-x)\ge 0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& y=0 \\
& -2\le x\le 1 \\
\end{aligned} \right.$
Vậy $M\left(z_1\right)$ thuộc đoạn $AB$ với $A(-2 ; 0), B(1 ; 0)$.
Mặt khác
$\left| i.{{z}_{2}}+3-2i \right|=2\Leftrightarrow \left| i\left( {{z}_{2}}+\dfrac{3}{i}-2 \right) \right|=2\Leftrightarrow \left| {{z}_{2}}-2-3i \right|=2$.
$N\left( {{z}_{2}} \right)$ thuộc đường tròn có tâm $I(2 ; 3), R=2$.Dấu bằng xảy ra khi $M \equiv A(-2 ; 0) \Rightarrow z_1=-2$ và $M \equiv A, I, N$ thẳng hàng theo thứ tự tức là
$\overrightarrow{IN}=\dfrac{IN}{AI}\overrightarrow{AI}=\dfrac{2}{5}(4;3)\Rightarrow N\left( \dfrac{18}{5};\dfrac{21}{5} \right)\Rightarrow {{z}_{2}}=\dfrac{18}{5}+\dfrac{21}{5}i$.
Khi đó $\left| i.{{z}_{1}}+{{z}_{2}}-1 \right|=\left| -2i+\dfrac{18}{5}+\dfrac{21}{5}i-1 \right|=\dfrac{\sqrt{290}}{5}$.Đáp án D.