Xét các số phức $\text{w}$, $z$ thỏa mãn $\left| \text{w}+i...

Cách 1.
Ta có: $5w=\left( 2+i \right)\left( z-4 \right)\Leftrightarrow 5w+5i=\left( 2+i \right)\left( z-4 \right)+5i$
$\Rightarrow \left| 5w+5i \right|=\left| \left( 2+i \right)\left( z-4 \right)+5i \right|\Rightarrow 5\left| w+i \right|=\left| \left( 1+2i \right)\left( z-4+1+2i \right) \right|=\sqrt{5}\left| z-3+2i \right|$
$\Rightarrow 5.\dfrac{3\sqrt{5}}{5}=\sqrt{5}\left| z-3+2i \right|\Rightarrow \left| z-3+2i \right|=3$.
Ta có:
${{\left| z+{{z}_{1}} \right|}^{2}}+{{\left| z-{{z}_{1}} \right|}^{2}}=2\left( {{\left| z \right|}^{2}}+{{\left| {{z}_{1}} \right|}^{2}} \right); \forall z, {{z}_{1}}$. (1)
${{\left| z \right|}^{2}}+{{\left| {{z}_{1}} \right|}^{2}}\ge \dfrac{{{\left( \left| z \right|+\left| {{z}_{1}} \right| \right)}^{2}}}{2}; \forall z, {{z}_{1}}$. (2)
Ta có: $P=\left| z-2i \right|+\left| z-6-2i \right|=\left| z-3-2i+3 \right|+\left| z-3-2i-3 \right|$.
Áp dụng (1) và (2), ta có:
${{\left| z-3-2i+3 \right|}^{2}}+{{\left| z-3-2i-3 \right|}^{2}}=2\left( {{\left| z-3-2i \right|}^{2}}+9 \right)$.
${{\left| z-3-2i+3 \right|}^{2}}+{{\left| z-3-2i-3 \right|}^{2}}\ge \dfrac{{{\left( \left| z-3-2i+3 \right|+\left| z-3-2i-3 \right| \right)}^{2}}}{2}=\dfrac{{{\left( \left| z-2i \right|+\left| z-6-2i \right| \right)}^{2}}}{2}$.
Vậy, ta có: $\dfrac{{{\left( \left| z-2i \right|+\left| z-6-2i \right| \right)}^{2}}}{2}\le 2\left( {{\left| z-3-2i \right|}^{2}}+9 \right)\Rightarrow {{\left( \left| z-2i \right|+\left| z-6-2i \right| \right)}^{2}}\le 4\left( {{\left| z-3-2i \right|}^{2}}+9 \right)$.
$\Rightarrow {{P}^{2}}\le 4\left( {{\left| z-3-2i \right|}^{2}}+9 \right)$.
Do $4\left( {{\left| z-3-2i \right|}^{2}}+9 \right)=4\left( {{\left| z-3+2i-4i \right|}^{2}}+9 \right)$ nên ${{P}^{2}}\le 4\left( {{\left( \left| z-3+2i \right|+\left| -4i \right| \right)}^{2}}+9 \right)$
$\Rightarrow {{P}^{2}}\le 4\left( {{7}^{2}}+9 \right)=232\Rightarrow P\le 2\sqrt{58}$.
Cách 2.
Ta có: $5w=\left( 2+i \right)\left( z-4 \right)$ thay $\left| \text{w}+i \right|=\dfrac{3\sqrt{5}}{5}$
$\Rightarrow \left| z-3+2i \right|=3$.
Suy ra, tập hợp các điểm biểu diễn số phức $z$ là đường tròn $\left( C \right): {{\left( x-3 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=9$.
Gọi $M\in \left( C \right)$.
Ta có: $P=\left| z-2i \right|+\left| z-6-2i \right|=AM+BM ; A\left( 0 ; 2 \right), B\left( 6 ; 2 \right)$.
Suy ra $P\le \sqrt{2\left( A{{M}^{2}}+B{{M}^{2}} \right)}$.
Gọi $H$ là trung điểm của cạnh $AB$.
Ta có: $P\le \sqrt{2\left( A{{M}^{2}}+B{{M}^{2}} \right)}=\sqrt{2\left( 2M{{H}^{2}}+\dfrac{A{{B}^{2}}}{2} \right)}=\sqrt{4M{{H}^{2}}+A{{B}^{2}}}$.
Vậy, $P=\left| z-2i \right|+\left| z-6-2i \right|$ đạt giá trị lớn nhất khi $M{{H}^{2}}$ đạt giá trị lớn nhất.
Dựa vào hình vẽ sau
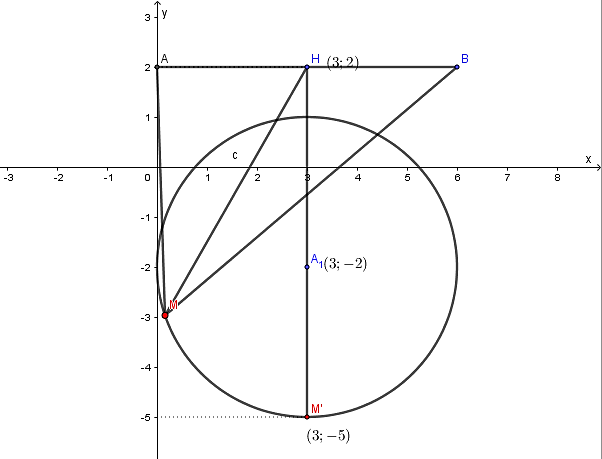Suy ra, $M{{H}^{2}}$ đạt giá trị lớn nhất khi $M\equiv M'$ $\Rightarrow {{P}^{2}}\le 232\Rightarrow P=2\sqrt{58}$.