Xét ba số phức $z_1, z_2, w$ thỏa mãn $\left(z_1-3 i\right)\left(i...

Giả sử $z_1=x+y i(x, y \in \mathbf{R})$, ta có:
$\left( {{z}_{1}}-3i \right)\left( i.{{z}_{1}}+i.{{{\bar{z}}}_{1}}-8 \right)=[x+(y-3)i][-8+2xi]=m+\left[ 2{{x}^{2}}-8(y-3) \right]i.$
Do $\left(z_1-3 i\right)\left(i . z_1+i \bar{z}_1-8\right)$ là số thực $\Rightarrow 2{{x}^{2}}-8\left( y-3 \right)=0\Leftrightarrow y=\dfrac{{{x}^{2}}}{4}+3(P)$.
Do đó tập hợp các điềm biểu diễn cùa $z_1$ là parabol $\left( P \right):y=\dfrac{{{x}^{2}}}{4}+3$.
Giả sử ${{z}_{2}}=a+bi,\text{w}={{x}_{1}}+{{y}_{1}}i,\left( {{x}_{1}},{{y}_{1}},a,b\in \mathbb{R} \right)$, ta có:
$\left| {{z}_{2}} \right|=\left| {{z}_{2}}-2-2i \right|\Leftrightarrow {{a}^{2}}+{{b}^{2}}={{(a-2)}^{2}}+{{(b-2)}^{2}}\Leftrightarrow a+b=2\ (1)$
$\dfrac{w-7-i}{{{z}_{2}}-7-i}=k(k\in \mathbb{R},k>0)\Leftrightarrow w=k\left( {{z}_{2}}-7-i \right)+7+i=(ka-7k+7)+(kb-k+1)i$
Từ (1) suy ra $w=(ka-7k+7)+(-ka+k+1)i\Rightarrow {{x}_{1}}=ka-7k+7;{{y}_{1}}=-ka+k+1$
$|w-7-i|=\dfrac{12}{\left|z_2-7-i\right|} \Leftrightarrow k\left|z_2-7-i\right|^2=12 \Leftrightarrow(k a-7 k)^2+(k b-k)^2=12 k$
$\Leftrightarrow\left(x_1-7\right)^2+\left(y_1-1\right)^2=12 k \Leftrightarrow\left(x_1-6\right)^2+y^2+\left(14-2 x_1-2 y_1-12 k\right)=0$
Vì $14-2 x_1-2 y_1-12 k=14-2(-6 k+8)-12 k=-2$ nên $\left(x_1-6\right)^2+y_1^2=2 \quad(C)$.
Do đó tập hơp các điểm biĉ̉u diễn của $w$ là đường tròn $(C)$.
Bài toán trở thành tìm $M(x, y) \in(P), N \in(C)$ sao cho $MN$ bé nhất.
Ta có $M N \geq M I-I N=M I-\sqrt{2}$ với $I(6 ; 0)$ là tâm đường tròn $(C)$.
Do đó $MN$ bé nhất khi và chỉ khi $MI$ bé nhất.
$M{{I}^{2}}={{(x-6)}^{2}}+{{\left( \dfrac{{{x}^{2}}}{4}+3 \right)}^{2}}.$
Đặt $f\left( x \right)={{(x-6)}^{2}}+{{\left( \dfrac{{{x}^{2}}}{4}+3 \right)}^{2}}\Rightarrow {f}'\left( x \right)=\dfrac{{{x}^{3}}}{4}+5x-12\Rightarrow {f}'\left( x \right)=0\Leftrightarrow x=2.$
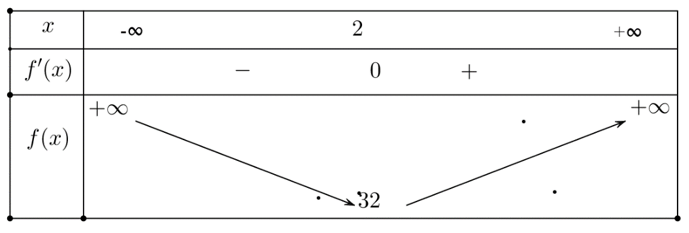$M{{I}^{2}}={{(x-6)}^{2}}+{{\left( \dfrac{{{x}^{2}}}{4}+3 \right)}^{2}}\ge 32\Rightarrow MI\ge 4\sqrt{2}\Rightarrow MN\ge 3\sqrt{2}\approx 4.25\in \left( 4;5 \right).$