Google
Câu hỏi: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A\left( 2;1;-3 \right)$, đường thẳng $\Delta : \dfrac{x-2}{1}= \dfrac{y-5}{-2}=\dfrac{z+3}{2}$ và mặt cầu $\left( S \right): {{\left( x-1 \right)}^{2}}+{{y}^{2}}+ {{\left( z-1 \right)}^{2}}= 25$. Mặt phẳng $\left( \alpha \right)$ thay đổi, luôn đi qua $A$ và song song với $\Delta $. Trong trường hợp $\left( \alpha \right)$ cắt mặt cầu $\left( S \right)$ theo một đường tròn có chu vi nhỏ nhất thì $\left( \alpha \right)$ có phương trình $ax+ by+ cz- 3= 0$. Tính giá trị của biểu thức $S= 3a-2b-2c$.
A. $12$.
B. $9$.
C. $4$.
D. $\dfrac{9}{5}$.
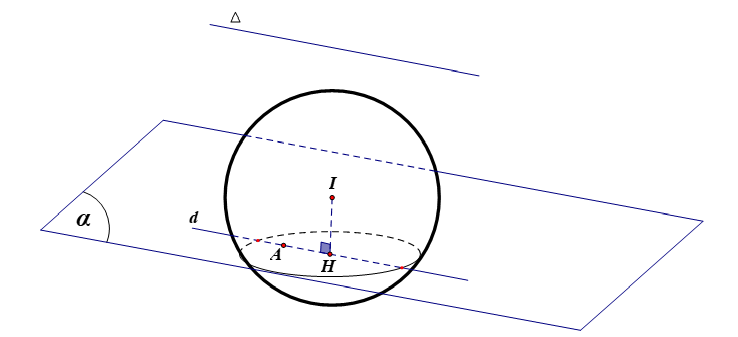Mặt cầu $\left( S \right)$ có tâm $I\left( 1;0;1 \right)$, bán kính $R=5$.
Dễ thấy $A$ nằm trong mặt cầu $\left( S \right)$ nên $\left( \alpha \right)$ luôn cắt $\left( S \right)$ theo một đường tròn $\left( C \right)$.
Đường thẳng $d$ đi qua $A$ và song song với $\Delta $ có phương trình là $\dfrac{x-2}{1}= \dfrac{y-1}{-2}=\dfrac{z+3}{2}$.
Gọi $H$ là hình chiếu của $I$ trên $d\Rightarrow H\left( 3;-1;-1 \right)$.
Gọi $r$ là bán kính của đường tròn $\left( C \right)$, ta có: ${{r}^{2}}={{R}^{2}}-{{\left[ d\left( I, \left( \alpha \right) \right) \right]}^{2}}\ge {{R}^{2}}-I{{H}^{2}}=16\Leftrightarrow r \ge 4$.
Chu vi của $\left( C \right)$ nhỏ nhất $\Leftrightarrow $ $r$ nhỏ nhất $\Leftrightarrow d\left( I, \left( \alpha \right) \right)= IH \Leftrightarrow H$ là hình chiếu của $I$ trên $\left( \alpha \right)$.
Khi đó, $\left( \alpha \right)$ đi qua $A$ và nhận $\overrightarrow{IH}\left( 2;-1;-2 \right)$ làm véc tơ pháp tuyến nên có phương trình:
Cách 2. Vì $(\alpha )//\Delta $ nên $a-2b+2c=0 (1).$
Vì $A(2;1;-3)\in (\alpha )$ nên $2\text{a}+b-3c-3=0 (2).$
Từ $(1)$ và $(2)$ suy ra $a=\dfrac{4c+6}{5}, b=\dfrac{7c+3}{5}.$
Điểm $A$ nằm bên trong mặt cầu $(S)$ nên mặt phẳng $(\alpha )$ luôn cắt mặt cầu theo giao tuyến là đường tròn có bán kính $r=\sqrt{25-{{h}^{2}}},$ với $h=\text{d}\left( I(1;0;1),mp(\alpha ) \right).$
Ta có $h=\dfrac{\left| a+c-3 \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=3.\sqrt{\dfrac{{{c}^{2}}-2c+1}{10{{c}^{2}}+10c+5}}.$
Với mọi $c\in \mathbb{R}$ ta có ${{(3c+2)}^{2}}\ge 0$
$\Leftrightarrow 9{{c}^{2}}+12c+4\ge 0\Leftrightarrow {{c}^{2}}-2c+1\le 10{{c}^{2}}+10c+5 (3).$
Mà $10{{c}^{2}}+10c+5>0,\forall c\in \mathbb{R},$ nên $(3)\Leftrightarrow \dfrac{{{c}^{2}}-2c+1}{10{{c}^{2}}+10c+5}\le 1.$ Dẫn tới $h\le 3,$ từ đó $r=\sqrt{25-{{h}^{2}}}\ge 4,$ dấu “=” xảy ra khi $c=-\dfrac{2}{3}.$
Vậy, đường tròn giao tuyến của $(S)$ và $(\alpha )$ có chu vi nhỏ nhất khi $c=-\dfrac{2}{3}\Rightarrow a=\dfrac{2}{3},b=-\dfrac{1}{3}\Rightarrow S=4.$
A. $12$.
B. $9$.
C. $4$.
D. $\dfrac{9}{5}$.
Dễ thấy $A$ nằm trong mặt cầu $\left( S \right)$ nên $\left( \alpha \right)$ luôn cắt $\left( S \right)$ theo một đường tròn $\left( C \right)$.
Đường thẳng $d$ đi qua $A$ và song song với $\Delta $ có phương trình là $\dfrac{x-2}{1}= \dfrac{y-1}{-2}=\dfrac{z+3}{2}$.
Gọi $H$ là hình chiếu của $I$ trên $d\Rightarrow H\left( 3;-1;-1 \right)$.
Gọi $r$ là bán kính của đường tròn $\left( C \right)$, ta có: ${{r}^{2}}={{R}^{2}}-{{\left[ d\left( I, \left( \alpha \right) \right) \right]}^{2}}\ge {{R}^{2}}-I{{H}^{2}}=16\Leftrightarrow r \ge 4$.
Chu vi của $\left( C \right)$ nhỏ nhất $\Leftrightarrow $ $r$ nhỏ nhất $\Leftrightarrow d\left( I, \left( \alpha \right) \right)= IH \Leftrightarrow H$ là hình chiếu của $I$ trên $\left( \alpha \right)$.
Khi đó, $\left( \alpha \right)$ đi qua $A$ và nhận $\overrightarrow{IH}\left( 2;-1;-2 \right)$ làm véc tơ pháp tuyến nên có phương trình:
$2x-y-2z-9=0 \Leftrightarrow \dfrac{2}{3}x-\dfrac{1}{3}y-\dfrac{2}{3}z-3=0$.
Từ đó, suy ra: $a=\dfrac{2}{3}, b=-\dfrac{1}{3}, c=-\dfrac{2}{3}\Rightarrow 3a-2b-2c=4$.Cách 2. Vì $(\alpha )//\Delta $ nên $a-2b+2c=0 (1).$
Vì $A(2;1;-3)\in (\alpha )$ nên $2\text{a}+b-3c-3=0 (2).$
Từ $(1)$ và $(2)$ suy ra $a=\dfrac{4c+6}{5}, b=\dfrac{7c+3}{5}.$
Điểm $A$ nằm bên trong mặt cầu $(S)$ nên mặt phẳng $(\alpha )$ luôn cắt mặt cầu theo giao tuyến là đường tròn có bán kính $r=\sqrt{25-{{h}^{2}}},$ với $h=\text{d}\left( I(1;0;1),mp(\alpha ) \right).$
Ta có $h=\dfrac{\left| a+c-3 \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=3.\sqrt{\dfrac{{{c}^{2}}-2c+1}{10{{c}^{2}}+10c+5}}.$
Với mọi $c\in \mathbb{R}$ ta có ${{(3c+2)}^{2}}\ge 0$
$\Leftrightarrow 9{{c}^{2}}+12c+4\ge 0\Leftrightarrow {{c}^{2}}-2c+1\le 10{{c}^{2}}+10c+5 (3).$
Mà $10{{c}^{2}}+10c+5>0,\forall c\in \mathbb{R},$ nên $(3)\Leftrightarrow \dfrac{{{c}^{2}}-2c+1}{10{{c}^{2}}+10c+5}\le 1.$ Dẫn tới $h\le 3,$ từ đó $r=\sqrt{25-{{h}^{2}}}\ge 4,$ dấu “=” xảy ra khi $c=-\dfrac{2}{3}.$
Vậy, đường tròn giao tuyến của $(S)$ và $(\alpha )$ có chu vi nhỏ nhất khi $c=-\dfrac{2}{3}\Rightarrow a=\dfrac{2}{3},b=-\dfrac{1}{3}\Rightarrow S=4.$
Đáp án C.