Google
Câu hỏi: Trong không gian $Oxyz$, khối đa diện $OAMEN$ có thể tích $296$ với các đỉnh $A\left( 0;0;8\sqrt{2} \right)$,
$M\left( 5;0;0 \right),N\left( 0;7;0 \right),E\left( a;b;0 \right)$, trong đó $a,b$ là các số thực dương. Khi $a,b$ thay đổi thì đường thằng $AE$ tiếp xúc với mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{c}^{2}}$. Mặt cầu $\left( S \right)$ có bán kính nhỏ nhất bằng
A. $\dfrac{24\sqrt{666}}{333}.$
B. $\dfrac{81\sqrt{37}}{74}.$
C. $\dfrac{27\sqrt{222}}{37}.$
D. $\dfrac{24\sqrt{74}}{\sqrt{461}}.$
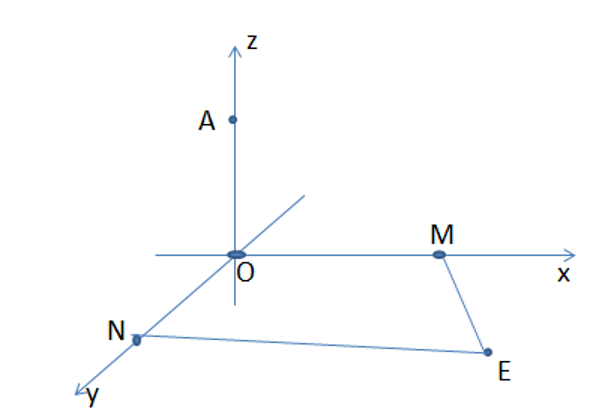Ta có bốn điểm $O,M,N,E$ cùng nằm trên mặt phẳng $\left( \text{Ox}y \right)$, ${{S}_{OMN}}=\dfrac{1}{2}OM.ON=\dfrac{35}{2}.$
${{V}_{OAMNE}}={{V}_{A.OM\text{E}N}}=\dfrac{1}{3}OA.{{S}_{OM\text{E}N}}=\dfrac{1}{3}.8\sqrt{2}.{{S}_{OM\text{E}N}}=296\Rightarrow {{S}_{OM\text{E}N}}=\dfrac{111}{\sqrt{2}}>{{S}_{OMN}}$
Do đó $E$ nằm ngoài tam giác $OMN$
${{S}_{OM\text{E}N}}={{S}_{OEM}}+{{S}_{OEN}}=\dfrac{1}{2}b.5+\dfrac{1}{2}a.7=\dfrac{7\text{a}+5b}{2}=\dfrac{111}{\sqrt{2}}\Rightarrow 7\text{a}+5b=111\sqrt{2}.$
Theo bất đẳng thức Bunhiacôpxki ta có:
${{\left( 111\sqrt{2} \right)}^{2}}={{\left( 7\text{a}+5b \right)}^{2}}\le \left( {{7}^{2}}+{{5}^{2}} \right)\left( {{a}^{2}}+{{b}^{2}} \right)\Leftrightarrow \left( {{a}^{2}}+{{b}^{2}} \right)\ge 333.$
Vì $A\text{E}$ tiếp xúc với mặt cầu tâm $O\left( 0;0;0 \right)$, bán kính $\left| c \right|$ nên
$\left| c \right|=d\left( O;A\text{E} \right)=\sqrt{\dfrac{O{{A}^{2}}.O{{E}^{2}}}{O{{A}^{2}}+O{{E}^{2}}}}=\sqrt{\dfrac{128.\left( {{a}^{2}}+{{b}^{2}} \right)}{{{a}^{2}}+{{b}^{2}}+128}}=\sqrt{128}.\sqrt{\dfrac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}+128}}\ge \sqrt{128}.\sqrt{\dfrac{333}{333+128}}=\dfrac{24\sqrt{74}}{\sqrt{461}}.$ (Do hàm số $f(t)=\dfrac{t}{t+128},\left( t\ge 333 \right)$ có ${f}'(t)=\dfrac{128}{{{\left( t+128 \right)}^{2}}}>0,\forall t\ge 333\Rightarrow f(t)$ đồng biến trên $\left[ 333;+\infty \right)$ ).
Vậy mặt cầu $\left( S \right)$ có bán kính nhỏ nhất bằng $\dfrac{24\sqrt{74}}{\sqrt{461}}$.
$M\left( 5;0;0 \right),N\left( 0;7;0 \right),E\left( a;b;0 \right)$, trong đó $a,b$ là các số thực dương. Khi $a,b$ thay đổi thì đường thằng $AE$ tiếp xúc với mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{c}^{2}}$. Mặt cầu $\left( S \right)$ có bán kính nhỏ nhất bằng
A. $\dfrac{24\sqrt{666}}{333}.$
B. $\dfrac{81\sqrt{37}}{74}.$
C. $\dfrac{27\sqrt{222}}{37}.$
D. $\dfrac{24\sqrt{74}}{\sqrt{461}}.$
${{V}_{OAMNE}}={{V}_{A.OM\text{E}N}}=\dfrac{1}{3}OA.{{S}_{OM\text{E}N}}=\dfrac{1}{3}.8\sqrt{2}.{{S}_{OM\text{E}N}}=296\Rightarrow {{S}_{OM\text{E}N}}=\dfrac{111}{\sqrt{2}}>{{S}_{OMN}}$
Do đó $E$ nằm ngoài tam giác $OMN$
${{S}_{OM\text{E}N}}={{S}_{OEM}}+{{S}_{OEN}}=\dfrac{1}{2}b.5+\dfrac{1}{2}a.7=\dfrac{7\text{a}+5b}{2}=\dfrac{111}{\sqrt{2}}\Rightarrow 7\text{a}+5b=111\sqrt{2}.$
Theo bất đẳng thức Bunhiacôpxki ta có:
${{\left( 111\sqrt{2} \right)}^{2}}={{\left( 7\text{a}+5b \right)}^{2}}\le \left( {{7}^{2}}+{{5}^{2}} \right)\left( {{a}^{2}}+{{b}^{2}} \right)\Leftrightarrow \left( {{a}^{2}}+{{b}^{2}} \right)\ge 333.$
Vì $A\text{E}$ tiếp xúc với mặt cầu tâm $O\left( 0;0;0 \right)$, bán kính $\left| c \right|$ nên
$\left| c \right|=d\left( O;A\text{E} \right)=\sqrt{\dfrac{O{{A}^{2}}.O{{E}^{2}}}{O{{A}^{2}}+O{{E}^{2}}}}=\sqrt{\dfrac{128.\left( {{a}^{2}}+{{b}^{2}} \right)}{{{a}^{2}}+{{b}^{2}}+128}}=\sqrt{128}.\sqrt{\dfrac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}+128}}\ge \sqrt{128}.\sqrt{\dfrac{333}{333+128}}=\dfrac{24\sqrt{74}}{\sqrt{461}}.$ (Do hàm số $f(t)=\dfrac{t}{t+128},\left( t\ge 333 \right)$ có ${f}'(t)=\dfrac{128}{{{\left( t+128 \right)}^{2}}}>0,\forall t\ge 333\Rightarrow f(t)$ đồng biến trên $\left[ 333;+\infty \right)$ ).
Vậy mặt cầu $\left( S \right)$ có bán kính nhỏ nhất bằng $\dfrac{24\sqrt{74}}{\sqrt{461}}$.
Đáp án D.