Trong không gian $Oxyz$, cho mặt cầu $\left( S \right):{{\left(...

Mặt cầu $\left( S \right)$ có tâm $I\left( 2;3;1 \right), R=\dfrac{1}{\sqrt{2}}$.
Gọi $d$ là đường thẳng đi qua hai điểm $A,B$.
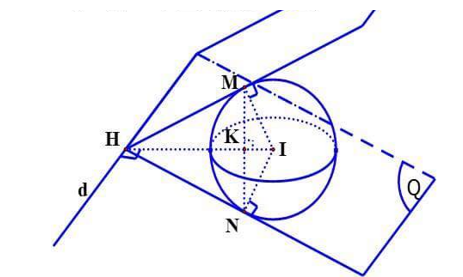
Gọi $M,N$ lần lượt là hai tiếp điểm của hai mặt phẳng vuông góc với nhau cùng đi qua $A,B$ và tiếp xúc với $\left( S \right)$ và $H$ là hình chiếu của $I$ lên $d$. Suy ra $IH=d\left( I,d \right)=1.$
Ta có $\Delta HMN$ vuông cân tại $H$ nên $\Delta MHI$ vuông tại $M$.
Ta có $\overrightarrow{IA}=\left( a-2;-3;-1 \right),\overrightarrow{AB}=\left( -a;b;0 \right)$
$IH=d\left( I,d \right)=\dfrac{\left| \left[ \overrightarrow{IA},\overrightarrow{AB} \right] \right|}{\left| \left[ \overrightarrow{AB} \right] \right|}=\dfrac{\sqrt{{{b}^{2}}+{{a}^{2}}+{{(ab-2b-3a)}^{2}}}}{\sqrt{{{b}^{2}}+{{a}^{2}}}}=1\Leftrightarrow ab-2b-3a=0\Leftrightarrow b=\dfrac{3a}{a-2}$
+ Với $a=0\Rightarrow b=0.$
+ Với $a\ne 0$ thì $a-2$ là ước của $3a$ nên có các trường hợp sau:
+ $\left[ \begin{matrix}
a-2=1 \\
a-2=-1 \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
a=3 \\
a=1 \\
\end{matrix} \right.$
+ $\left[ \begin{matrix}
a-2=a \\
a-2=-a \\
\end{matrix} \right.\Leftrightarrow a=1$
+ $\left[ \begin{matrix}
a-2=3 \\
a-2=-3 \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
a=5 \\
a=-1 \\
\end{matrix} \right.$
+ $\left[ \begin{matrix}
a-2=3a \\
a-2=-3a \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
a=-1 \\
a=\dfrac{1}{2}(l) \\
\end{matrix} \right.$
Vậy có $5$ giá trị $a$ thỏa mãn là $a=-1,a=0,a=1,a=3,a=5$ nên có $5$ cặp thỏa mãn.