Google
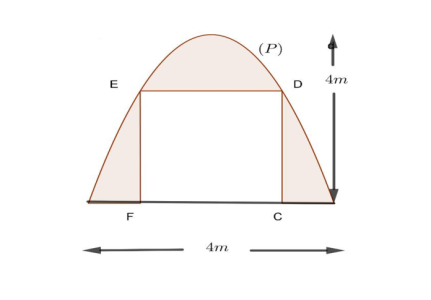
Câu hỏi: Một chiếc cổng có dạng là một parabol $\left( P \right)$ có kích thước như hình vẽ, biết chiều cao cổng bằng $4 m , AB = 4 m$. Người ta thiết kế cửa đi là một hình chữ nhật $CDEF $, phần còn lại dùng để trang trí. Biết chi phí phần tô đậm là 1.000.000 đồng/ ${{m}^{2}}$. Hỏi số tiền ít nhất dùng để trang trí phần tô đậm gần với số tiền nào dưới đây?
A. 4.450.000 đồng.
B. 4605.000 đồng.
C. 4.505.000 đồng.
D. 4.509.000 đồng.
B. 4605.000 đồng.
C. 4.505.000 đồng.
D. 4.509.000 đồng.
Trước hết, ta chọn hệ trục tọa độ $Oxy$, như hình vẽ
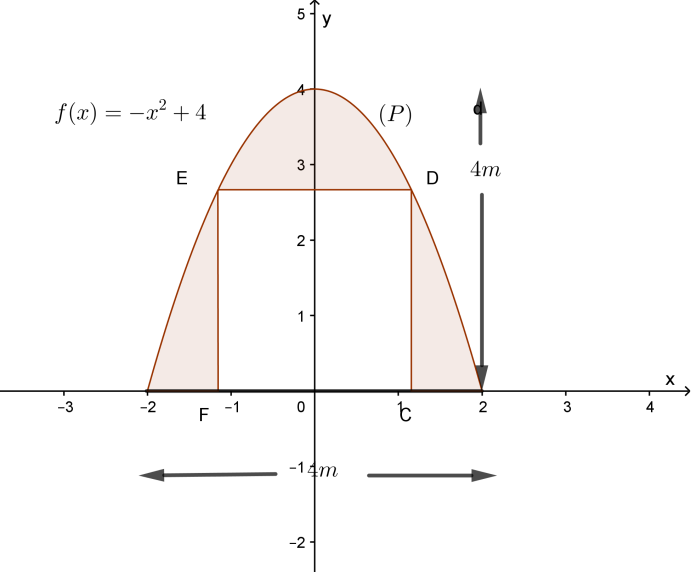Từ hình vẽ, ta có parabol $\left( P \right)$ có dạng: $y=a{{x}^{2}}+b ; a , b \in \mathbb{R}$.
Do $\left( P \right)$ qua hai điểm có tọa độ là $\left( 2 ; 0 \right) , \left( 0 ; 4 \right)$ nên $\left( P \right)$ có phương trình $y=-{{x}^{2}}+4$.
Ta có, diện tích của $\left( P \right)$ tạo với trục hoành là: $S=\int_{-2}^{2}{\left( -{{x}^{2}}+4 \right)\text{d}}x=\dfrac{32}{3} {{m}^{2}}$.
Ta gọi điểm $C\left( a ; 0 \right)\Rightarrow D\left( 0 ; -{{a}^{2}}+4 \right) ; 0<a<2$.
Do đó, diện tích của hình chữ nhật $CDEF$ là: ${{S}_{CDEF}} = 2a\left( 4-{{a}^{2}} \right)=8a-2{{a}^{3}}$.
Theo đề bài, để phần trang trí, có chi phí nhỏ nhất thì diện tích của hình chữ nhật $CDEF$ đạt giá trị lớn nhất.
Do cổng chào đối xứng qua trục tung nên ta đặt: $g\left( a \right)=\dfrac{{{S}_{CDEF}}}{2}=4a-{{a}^{3}} , 0<a<2$.
$\Rightarrow g'\left( a \right)=4-3{{a}^{2}} \Rightarrow g'\left( a \right)=0\Rightarrow a=\dfrac{2\sqrt{3}}{3}$.
Ta có, BBT:
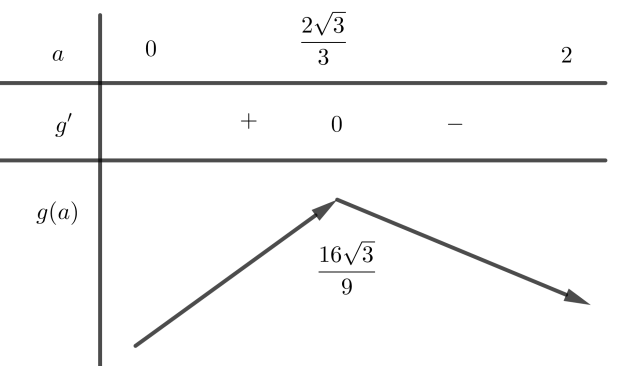Dựa vào bảng biến thiên, suy ra diện tích hình chữ nhật $CDEF$ đạt giá trị lớn nhất là
$\dfrac{32\sqrt{3}}{9} {{m}^{2}}$. Vậy, diện tích nhỏ nhất của phần dùng để trang trí là $\dfrac{96-32\sqrt{3}}{9} {{m}^{2}}$.
Do đó, số tiền ít nhất dùng để trang trí phần tô đậm là $\left( \dfrac{96-32\sqrt{3}}{9} \right).1000000= 4508263,795\approx 4.509.000$ đồng/ ${{m}^{2}}$.
Do $\left( P \right)$ qua hai điểm có tọa độ là $\left( 2 ; 0 \right) , \left( 0 ; 4 \right)$ nên $\left( P \right)$ có phương trình $y=-{{x}^{2}}+4$.
Ta có, diện tích của $\left( P \right)$ tạo với trục hoành là: $S=\int_{-2}^{2}{\left( -{{x}^{2}}+4 \right)\text{d}}x=\dfrac{32}{3} {{m}^{2}}$.
Ta gọi điểm $C\left( a ; 0 \right)\Rightarrow D\left( 0 ; -{{a}^{2}}+4 \right) ; 0<a<2$.
Do đó, diện tích của hình chữ nhật $CDEF$ là: ${{S}_{CDEF}} = 2a\left( 4-{{a}^{2}} \right)=8a-2{{a}^{3}}$.
Theo đề bài, để phần trang trí, có chi phí nhỏ nhất thì diện tích của hình chữ nhật $CDEF$ đạt giá trị lớn nhất.
Do cổng chào đối xứng qua trục tung nên ta đặt: $g\left( a \right)=\dfrac{{{S}_{CDEF}}}{2}=4a-{{a}^{3}} , 0<a<2$.
$\Rightarrow g'\left( a \right)=4-3{{a}^{2}} \Rightarrow g'\left( a \right)=0\Rightarrow a=\dfrac{2\sqrt{3}}{3}$.
Ta có, BBT:
$\dfrac{32\sqrt{3}}{9} {{m}^{2}}$. Vậy, diện tích nhỏ nhất của phần dùng để trang trí là $\dfrac{96-32\sqrt{3}}{9} {{m}^{2}}$.
Do đó, số tiền ít nhất dùng để trang trí phần tô đậm là $\left( \dfrac{96-32\sqrt{3}}{9} \right).1000000= 4508263,795\approx 4.509.000$ đồng/ ${{m}^{2}}$.
Đáp án D.