Google
Câu hỏi: Cho Parabol $\left( P \right):y=-{{x}^{2}}+4x$ có đỉnh $I$ và $A$ là giao điểm khác $O$ của $\left( P \right)$ với trục hoành. $M$ là điểm bất kì trên cung $IA$, tiếp tuyến của $\left( P \right)$ tại $M$ cắt $\text{Ox}, Oy$ lần lượt tại $B, C$. Gọi ${{S}_{1}},{{S}_{2}}$ lần lượt là diện tích của hai tam giác cong $MAB, MOC$. Tìm $M$ sao cho ${{S}_{1}}+{{S}_{2}}$ nhỏ nhất.
A. $M\left( 4 ; 0 \right)$.
B. $M\left( 3 ; 3 \right)$.
C. $M\left( \dfrac{8}{3} ; \dfrac{32}{9} \right)$.
D. $M\left( \dfrac{8}{3} ; \dfrac{160}{9} \right)$.
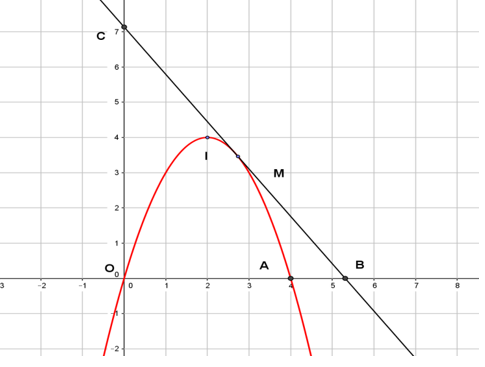Vì $M$ thuộc cung $IA$ nên giả sử $M\left( m ; -{{m}^{2}}+4m \right)$ với $2<m\le 4$.
Tiếp tuyến tại $M$ có phương trình: $y=(-2m+4)x+{{m}^{2}}$.
Khi đó $B\left( \dfrac{{{m}^{2}}}{2m-4};0 \right), C\left( 0;{{m}^{2}} \right)$.
Gọi ${{S}_{3}}$ là diện tích giới hạn bởi $\left( P \right)$ và Ox, ta có ${{S}_{3}}=\int\limits_{0}^{4}{\left( -{{x}^{2}}+4x \right)}dx=\dfrac{32}{3}$.
Diện tích tam giác vuông $OBC$ là $S=\dfrac{1}{2}OB.OC=\dfrac{{{m}^{4}}}{4\left( m-2 \right)}$.
Ta có: ${{S}_{1}}+{{S}_{2}}=S-{{S}_{3}}=\dfrac{{{m}^{4}}}{4\left( m-2 \right)}-\dfrac{32}{3}$.
Suy ra ${{S}_{1}}+{{S}_{2}}$ nhỏ nhất khi và chỉ khi $S=f\left( m \right)=\dfrac{{{m}^{4}}}{4\left( m-2 \right)}$ nhỏ nhất.
Ta có $f'\left( m \right)=\dfrac{{{m}^{3}}\left( 3m-8 \right)}{4{{\left( m-2 \right)}^{2}}}, f'\left( m \right)=0\Leftrightarrow m=\dfrac{8}{3}$.
Lập BBT ta được $f\left( m \right)$ nhỏ nhất khi $m=\dfrac{8}{3}$.
Vậy ${{S}_{1}}+{{S}_{2}}$ nhỏ nhất khi $M\left( \dfrac{8}{3} ; \dfrac{32}{9} \right)$.
A. $M\left( 4 ; 0 \right)$.
B. $M\left( 3 ; 3 \right)$.
C. $M\left( \dfrac{8}{3} ; \dfrac{32}{9} \right)$.
D. $M\left( \dfrac{8}{3} ; \dfrac{160}{9} \right)$.
Tiếp tuyến tại $M$ có phương trình: $y=(-2m+4)x+{{m}^{2}}$.
Khi đó $B\left( \dfrac{{{m}^{2}}}{2m-4};0 \right), C\left( 0;{{m}^{2}} \right)$.
Gọi ${{S}_{3}}$ là diện tích giới hạn bởi $\left( P \right)$ và Ox, ta có ${{S}_{3}}=\int\limits_{0}^{4}{\left( -{{x}^{2}}+4x \right)}dx=\dfrac{32}{3}$.
Diện tích tam giác vuông $OBC$ là $S=\dfrac{1}{2}OB.OC=\dfrac{{{m}^{4}}}{4\left( m-2 \right)}$.
Ta có: ${{S}_{1}}+{{S}_{2}}=S-{{S}_{3}}=\dfrac{{{m}^{4}}}{4\left( m-2 \right)}-\dfrac{32}{3}$.
Suy ra ${{S}_{1}}+{{S}_{2}}$ nhỏ nhất khi và chỉ khi $S=f\left( m \right)=\dfrac{{{m}^{4}}}{4\left( m-2 \right)}$ nhỏ nhất.
Ta có $f'\left( m \right)=\dfrac{{{m}^{3}}\left( 3m-8 \right)}{4{{\left( m-2 \right)}^{2}}}, f'\left( m \right)=0\Leftrightarrow m=\dfrac{8}{3}$.
Lập BBT ta được $f\left( m \right)$ nhỏ nhất khi $m=\dfrac{8}{3}$.
Vậy ${{S}_{1}}+{{S}_{2}}$ nhỏ nhất khi $M\left( \dfrac{8}{3} ; \dfrac{32}{9} \right)$.
Đáp án C.
