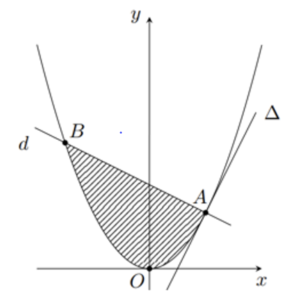
Trong mặt phẳng $Oxy$, cho parabol $\left( P \right):y={{x}^{2}}$...

$\left( P \right):y={{x}^{2}}$ $\Rightarrow {y}'=2x$.
Tiếp tuyến $\Delta $ có hệ số góc ${{k}_{\Delta }}={y}'\left( a \right)=2a$. Đường thẳng $d$ có hệ số góc ${{k}_{d}}$.
Theo đề ta có: $d\bot \Delta \Leftrightarrow {{k}_{\Delta }}.{{k}_{d}}=-1$ $\Leftrightarrow {{k}_{d}}=-\dfrac{1}{{{k}_{\Delta }}}=-\dfrac{1}{2a}$.
Phương trình đường thẳng $d:y=-\dfrac{1}{2a}\left( x-a \right)+{{a}^{2}}$ $\Leftrightarrow d:y=-\dfrac{1}{2a}x+{{a}^{2}}+\dfrac{1}{2}$.
Phương tình hoành độ giao điểm của $\left( P \right)\And d$.
${{x}^{2}}=-\dfrac{1}{2a}x+{{a}^{2}}+\dfrac{1}{2}$ $\Leftrightarrow {{x}^{2}}+\dfrac{1}{2a}x-{{a}^{2}}-\dfrac{1}{2}=0$.
$\Leftrightarrow {{x}_{1}}=-a-\dfrac{1}{2a}\cup {{x}_{2}}=a$.
Dựa vào hình vẽ, ta có diện tích cần tìm là
$S=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\left[ \left( -\dfrac{1}{2a}x+{{a}^{2}}+\dfrac{1}{2} \right)-{{x}^{2}} \right]dx}$ $=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\left( -{{x}^{2}}-\dfrac{1}{2a}x+{{a}^{2}}+\dfrac{1}{2} \right)dx}$
$S=\left. \left( -\dfrac{1}{3}{{x}^{3}}-\dfrac{1}{4a}{{x}^{2}}+\left( {{a}^{2}}+\dfrac{1}{2} \right)x \right) \right|_{{{x}_{1}}}^{{{x}_{2}}}$ $=\left. \left( -\dfrac{1}{3}{{x}^{3}}-\dfrac{1}{4a}{{x}^{2}}+\left( {{a}^{2}}+\dfrac{1}{2} \right)x \right) \right|_{-a-\dfrac{1}{2a}}^{a}$
$S=\dfrac{4}{3}{{a}^{3}}+a+\dfrac{1}{4a}+\dfrac{1}{48{{a}^{3}}}$ $=\left( \dfrac{4}{3}{{a}^{3}}+\dfrac{1}{12a}+\dfrac{1}{12a}+\dfrac{1}{12a} \right)+\left( \dfrac{a}{3}+\dfrac{a}{3}+\dfrac{a}{3}+\dfrac{1}{48{{a}^{3}}} \right)$
$S\overset{Cauchy}{\mathop{\ge }} 4.\sqrt[4]{\dfrac{4}{3}{{a}^{3}}.\dfrac{1}{12a}.\dfrac{1}{12a}.\dfrac{1}{12a}}+4.\sqrt[4]{\dfrac{a}{3}.\dfrac{a}{3}.\dfrac{a}{3}.\dfrac{1}{48{{a}^{3}}}}$ $=\dfrac{4}{3}$.
Vậy $MinS=\dfrac{4}{3}$ $\Leftrightarrow \left\{ \begin{aligned}
& \dfrac{4{{a}^{3}}}{3}=\dfrac{1}{12a} \\
& \dfrac{a}{3}=\dfrac{1}{48{{a}^{3}}} \\
\end{aligned} \right.$$\Leftrightarrow {{a}^{4}}=\dfrac{1}{16}\Leftrightarrow a=\dfrac{1}{2}$.
CÁCH KHÁC
Làm tương tự cách trên, ta có $d$ cắt $\left( P \right)$ lần lượt tại $A\left( a;{{a}^{2}} \right);B\left( -a-\dfrac{1}{2a};{{\left( a+\dfrac{1}{2a} \right)}^{2}} \right)$.
Gọi $I$ là điểm thuộc $\left( P \right)$ sao cho ${{x}_{I}}=\dfrac{{{x}_{A}}+{{x}_{B}}}{2}\Rightarrow I\left( -\dfrac{1}{4a};\dfrac{1}{16{{a}^{2}}} \right)$.
Ta có ngay: $\left\{ \begin{aligned}
& \overrightarrow{AB}=\left( -2a-\dfrac{1}{2a};1+\dfrac{1}{4{{a}^{2}}} \right) \\
& \overrightarrow{AI}=\left( -\dfrac{1}{4a}-a;\dfrac{1}{16{{a}^{2}}}-{{a}^{2}} \right) \\
\end{aligned} \right.$.
$\Rightarrow {{S}_{\Delta IAB}}=\dfrac{1}{2}\left| \left( -2a-\dfrac{1}{2a} \right)\left( \dfrac{1}{16{{a}^{2}}}-{{a}^{2}} \right)-\left( 1+\dfrac{1}{4{{a}^{2}}} \right)\left( -\dfrac{1}{4a}-a \right) \right|$
$\Rightarrow {{S}_{\Delta IAB}}={{a}^{3}}+\dfrac{3}{4}a+\dfrac{3}{16a}+\dfrac{1}{64{{a}^{3}}}$.
Diện tích hình phẳng giới hạn bởi $d$ và $\left( P \right)$ là
$S=\dfrac{4}{3}{{S}_{\Delta IAB}}=\dfrac{4}{3}{{a}^{3}}+a+\dfrac{1}{4a}+\dfrac{1}{48{{a}^{3}}}$.
$S=\left( \dfrac{4}{3}{{a}^{3}}+\dfrac{1}{12a}+\dfrac{1}{12a}+\dfrac{1}{12a} \right)+\left( \dfrac{a}{3}+\dfrac{a}{3}+\dfrac{a}{3}+\dfrac{1}{48{{a}^{3}}} \right)$
$S\overset{Cauchy}{\mathop{\ge }} 4.\sqrt[4]{\dfrac{4}{3}{{a}^{3}}.\dfrac{1}{12a}.\dfrac{1}{12a}.\dfrac{1}{12a}}+4.\sqrt[4]{\dfrac{a}{3}.\dfrac{a}{3}.\dfrac{a}{3}.\dfrac{1}{48{{a}^{3}}}}$ $=\dfrac{4}{3}$.
Vậy $MinS=\dfrac{4}{3}$ $\Leftrightarrow \left\{ \begin{aligned}
& \dfrac{4{{a}^{3}}}{3}=\dfrac{1}{12a} \\
& \dfrac{a}{3}=\dfrac{1}{48{{a}^{3}}} \\
\end{aligned} \right.$$\Leftrightarrow {{a}^{4}}=\dfrac{1}{16}\Leftrightarrow a=\dfrac{1}{2}$.