Gọi $S$ là tập hợp tất cả các số phức $z$ sao cho...

Giả sử $z=x+yi,\ \left( x,\ y\in \mathbb{R} \right)$. Ta có
$iz.\bar{z}+\left( 1+2i \right)z-\left( 1-2i \right)\bar{z}-4i=0$
$\begin{aligned}
& \Leftrightarrow i\left( x+yi \right)\left( x-yi \right)+\left( 1+2i \right)\left( x+yi \right)-\left( 1-2i \right)\left( x-yi \right)-4i=0 \\
& \Leftrightarrow i\left( {{x}^{2}}+{{y}^{2}} \right)+\left( x-2y \right)+\left( 2x+y \right)i-\left( x-2y \right)-\left( -2x-y \right)i-4i=0 \\
& \Leftrightarrow {{x}^{2}}+{{y}^{2}}+4x+2y-4=0 \\
\end{aligned}$
Suy ra $S$ là tập hợp các số phức có điểm biểu diễn thuộc đường tròn $\left( C \right)$ có tâm $I\left( -2\ ;\ -1 \right)$, bán kính $R=3$.
Giả sử $w=a+bi,\ \left( a,\ b\in \mathbb{R};\ a\ne 0 \right)$. Ta có
$\dfrac{w}{\overline{w}+6i}=\dfrac{a+bi}{a+\left( 6-b \right)i}=\dfrac{\left( a+bi \right)\left[ a+\left( b-6 \right)i \right]}{{{a}^{2}}+{{\left( b-6 \right)}^{2}}}=\dfrac{{{a}^{2}}-{{b}^{2}}+6b}{{{a}^{2}}+{{\left( 6-b \right)}^{2}}}+\dfrac{2ab-6a}{{{a}^{2}}+{{\left( 6-b \right)}^{2}}}i$
Do đó $\dfrac{w}{\overline{w}+6i}$ là số thực khi và chỉ khi $\dfrac{2ab-6a}{{{a}^{2}}+{{\left( 6-b \right)}^{2}}}=0\Leftrightarrow b=3$.
Suy ra $T$ là tập hợp các số phức có điểm biểu diễn thuộc đường thẳng $\Delta :y=3$.
Xét các số phức ${{z}_{1}},\ {{z}_{2}}\in S$ và $w\in T$ thỏa mãn $\left| {{z}_{1}}-{{z}_{2}} \right|=\sqrt{5}$ và $\dfrac{w-{{z}_{1}}}{{{z}_{2}}-{{z}_{1}}}=\dfrac{\overline{w}-\overline{{{z}_{1}}}}{\overline{{{z}_{2}}}-{{\overline{z}}_{1}}}$.
Giả sử ${{z}_{1}}={{x}_{1}}+{{y}_{1}}i,\ {{z}_{2}}={{x}_{2}}+{{y}_{2}}i\ \left( {{x}_{1}},\ {{y}_{1}},\ {{x}_{2}},\ {{y}_{2}}\in \mathbb{R} \right)$ và $w=x+3i,\ \left( x\in \mathbb{R},\ x\ne 0 \right)$.
Gọi ${{M}_{1}},\ {{M}_{2}},\ M$ lần lượt là các điểm biểu diễn của ${{z}_{1}},\ {{z}_{2}}$ và $w$.
Khi đó, ${{M}_{1}},\ {{M}_{2}}\in \left( C \right)$ và $M\in \Delta $, đồng thời $\left| w-{{z}_{1}} \right|.\left| w-{{z}_{1}} \right|=M{{M}_{1}}.M{{M}_{2}}$.
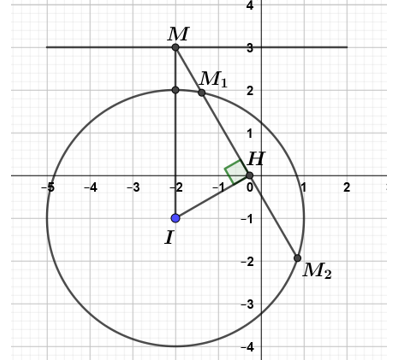Do $\left| {{z}_{1}}-{{z}_{2}} \right|=2\sqrt{5}$ nên ${{M}_{1}}{{M}_{2}}=2\sqrt{5}$ và do $\dfrac{w-{{z}_{1}}}{{{z}_{2}}-{{z}_{1}}}=\dfrac{\overline{w}-\overline{{{z}_{1}}}}{\overline{{{z}_{2}}}-{{\overline{z}}_{1}}}$ nên ba điểm ${{M}_{1}},\ {{M}_{2}},\ M$ thẳng hàng.
Suy ra $M{{M}_{1}}.M{{M}_{2}}=I{{M}^{2}}-{{R}^{2}}$.
Vì vậy $\left| w-{{z}_{1}} \right|.\left| w-{{z}_{1}} \right|=I{{M}^{2}}-{{R}^{2}}$.
Do đó, $\left| w-{{z}_{1}} \right|.\left| w-{{z}_{1}} \right|$ đạt giá trị nhỏ nhất khi và chỉ khi $IM$ đạt giá trị nhỏ nhất. Lúc đó, $M$ là hình chiếu vuông góc của $I$ trên $\Delta $ và $M=\left( -2\ ;\ 3 \right)$.
Gọi $H$ là trung điểm của ${{M}_{1}}{{M}_{2}}$, ta có $IH=\sqrt{IM_{1}^{2}-{{M}_{1}}{{H}^{2}}}=\sqrt{{{3}^{2}}-{{\left( \sqrt{5} \right)}^{2}}}=2$.
Vì bốn điểm ${{M}_{1}},\ {{M}_{2}},\ M,\ H$ thẳng hàng nên $\Delta MIH$ vuông tại $H$ suy ra $MH=\sqrt{I{{M}^{2}}-I{{H}^{2}}}=\sqrt{{{4}^{2}}-{{2}^{2}}}=2\sqrt{3}$ và do đó,
$\left| w-{{z}_{1}} \right|+\left| w-{{z}_{1}} \right|=M{{M}_{1}}+M{{M}_{2}}=MH-H{{M}_{1}}+MH+H{{M}_{2}}=2MH=4\sqrt{3}$.