Google
Câu hỏi: Gọi $S$ là tập hợp các số phức $z$ thỏa mãn $z.\overline{z}=\left| z+\overline{z} \right|$. Xét các số phức ${{z}_{1}};{{z}_{2}}\in S$ sao cho $\left| {{z}_{1}}-{{z}_{2}} \right|=1$. Giá trị nhỏ nhất của biểu thức $P=\left| {{z}_{1}}-\sqrt{3}i \right|+\left| \overline{{{z}_{2}}}+\sqrt{3}i \right|$ bằng
A. $2$.
B. $\sqrt{20-8\sqrt{3}}$.
C. $2\sqrt{3}$.
D. $1+\sqrt{3}$.
Đặt $z=x+iy \left( x,y\in \mathbb{R} \right)$. Phương trình $z.\overline{z}=\left| z+\overline{z} \right|$ trở thành ${{x}^{2}}+{{y}^{2}}=2\left| x \right|\Leftrightarrow \left[ \begin{aligned}
& {{\left( x-1 \right)}^{2}}+{{y}^{2}}=1 \\
& {{\left( x+1 \right)}^{2}}+{{y}^{2}}=1 \\
\end{aligned} \right.$
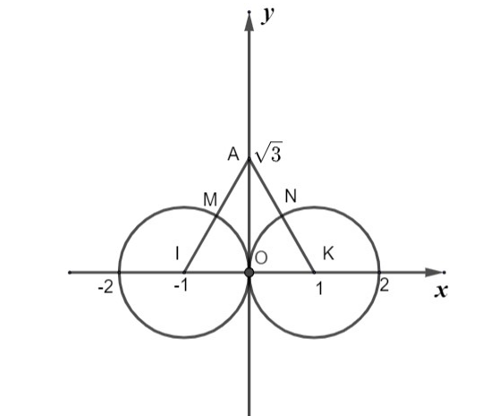
Suy ra điểm biểu diễn của ${{z}_{1}};{{z}_{2}}$ nằm trên đường tròn tâm $I$, tâm $K$ bán kính 1.
$P=\left| {{z}_{1}}-\sqrt{3}i \right|+\left| \overline{{{z}_{2}}}+\sqrt{3}i \right|=\left| {{z}_{1}}-\sqrt{3}i \right|+\left| {{z}_{2}}-\sqrt{3}i \right|=AD+AE$ với $A\left( 0;\sqrt{3} \right)$ và $D,E$ là điểm biểu diễn của ${{z}_{1}};{{z}_{2}}$. Vì $D,E$ nằm trên các đường tròn tâm $I$, tâm $K$ nên $AD+AE\ge AM+AN\ge 2$, dấu “=” xảy ra khi $D$ và $E$ ở các vị trí $M$ và $N$. Khi đó $M,N$ là trung điểm của $AI,AK$ nên $\left| {{z}_{1}}-{{z}_{2}} \right|=MN=\dfrac{1}{2}IK=1$
A. $2$.
B. $\sqrt{20-8\sqrt{3}}$.
C. $2\sqrt{3}$.
D. $1+\sqrt{3}$.
& {{\left( x-1 \right)}^{2}}+{{y}^{2}}=1 \\
& {{\left( x+1 \right)}^{2}}+{{y}^{2}}=1 \\
\end{aligned} \right.$
Suy ra điểm biểu diễn của ${{z}_{1}};{{z}_{2}}$ nằm trên đường tròn tâm $I$, tâm $K$ bán kính 1.
$P=\left| {{z}_{1}}-\sqrt{3}i \right|+\left| \overline{{{z}_{2}}}+\sqrt{3}i \right|=\left| {{z}_{1}}-\sqrt{3}i \right|+\left| {{z}_{2}}-\sqrt{3}i \right|=AD+AE$ với $A\left( 0;\sqrt{3} \right)$ và $D,E$ là điểm biểu diễn của ${{z}_{1}};{{z}_{2}}$. Vì $D,E$ nằm trên các đường tròn tâm $I$, tâm $K$ nên $AD+AE\ge AM+AN\ge 2$, dấu “=” xảy ra khi $D$ và $E$ ở các vị trí $M$ và $N$. Khi đó $M,N$ là trung điểm của $AI,AK$ nên $\left| {{z}_{1}}-{{z}_{2}} \right|=MN=\dfrac{1}{2}IK=1$
Đáp án A.