Google
Câu hỏi: Có bao nhiêu số thực $y$ thuộc khoảng $\left( -\ \dfrac{1}{5}\ ;\ \dfrac{1}{5} \right)$ sao cho ứng mỗi $y$ có duy nhất số thực $x$ thỏa mãn ${{\log }_{2}}\left( 3{{x}^{2}}+10xy+20{{y}^{2}} \right)={{\log }_{5}}\left( {{x}^{2}}+2xy+3{{y}^{2}} \right)$ ?
A. 2.
B. 4.
C. 6.
D. 8.
A. 2.
B. 4.
C. 6.
D. 8.
Điều kiện: $\left\{ \begin{aligned}
& 3{{x}^{2}}+10xy+20{{y}^{2}}>0 \\
& {{x}^{2}}+2xy+3{{y}^{2}}>0 \\
\end{aligned} \right.$.
Đặt ${{\log }_{2}}\left( 3{{x}^{2}}+10xy+20{{y}^{2}} \right)={{\log }_{5}}\left( {{x}^{2}}+2xy+3{{y}^{2}} \right)=m$. Ta có hệ
$\left\{ \begin{aligned}
& 3{{x}^{2}}+10xy+20{{y}^{2}}={{2}^{m}} \\
& {{x}^{2}}+2xy+3{{y}^{2}}={{5}^{m}} \\
\end{aligned} \right.\quad \left( * \right)$
Nếu $y=0$ thì $\left\{ \begin{aligned}
& 3{{x}^{2}}={{2}^{m}} \\
& {{x}^{2}}={{5}^{m}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& {{x}^{2}}={{5}^{m}} \\
& {{3.5}^{m}}={{2}^{m}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m={{\log }_{\dfrac{2}{5}}}3 \\
& x=\pm \sqrt{{{5}^{{{\log }_{\dfrac{2}{5}}}3}}} \\
\end{aligned} \right. $. Suy ra có hai số thực $ x$ thỏa mãn.
Nếu $y\ne 0$ thì đặt $x=ty,\ \left( t\in \mathbb{R} \right)$. Hệ trên trở thành $\left\{ \begin{aligned}
& {{y}^{2}}\left( 3{{t}^{2}}+10t+20 \right)={{2}^{m}}\quad \left( 1 \right) \\
& {{y}^{2}}\left( {{t}^{2}}+2t+3 \right)={{5}^{m}}\quad \quad \ \left( 2 \right) \\
\end{aligned} \right.$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $\dfrac{3{{t}^{2}}+10t+20}{{{t}^{2}}+2t+3}={{\left( \dfrac{2}{5} \right)}^{m}}\quad \left( ** \right)$
Từ cách đặt suy ra ứng mỗi $y$ có duy nhất số thực $x$ khi và chỉ khi $\left( ** \right)$ có nghiệm duy nhất.
Xét hàm số $f\left( t \right)=\dfrac{3{{t}^{2}}+10t+20}{{{t}^{2}}+2t+3}$. Ta có ${f}'\left( t \right)=\dfrac{-2\left( 2{{t}^{2}}+11t+5 \right)}{{{\left( {{t}^{2}}+2t+3 \right)}^{2}}};$ ${f}'\left( t \right)=0\Leftrightarrow \left[ \begin{aligned}
& t=-5 \\
& t=-\ \dfrac{1}{2} \\
\end{aligned} \right.$.
Bảng biến thiên:
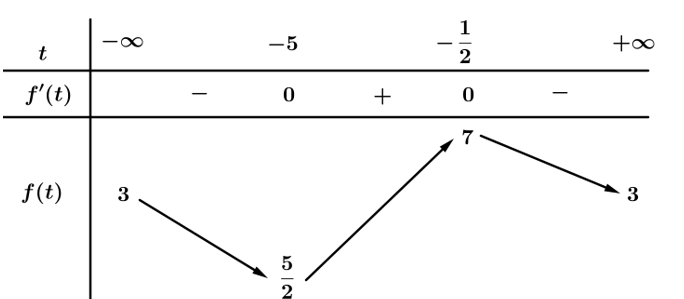Từ bảng biến thiên suy ra $\left( ** \right)$ có nghiệm duy nhất khi và chỉ khi $\left[ \begin{aligned}
& {{\left( \dfrac{2}{5} \right)}^{m}}=7 \\
& {{\left( \dfrac{2}{5} \right)}^{m}}=3 \\
& {{\left( \dfrac{2}{5} \right)}^{m}}=\dfrac{5}{2} \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& m={{\log }_{\dfrac{2}{5}}}7 \\
& m={{\log }_{\dfrac{2}{5}}}3 \\
& m=-1 \\
\end{aligned} \right.$
Trường hợp 1 : $m={{\log }_{\dfrac{2}{5}}}7$. Khi đó $\left( ** \right)$ có nghiệm duy nhất $t=-\ \dfrac{1}{2}$.
Thay vào $\left( 2 \right)$ ta được ${{y}^{2}}=\dfrac{{{4.5}^{{{\log }_{\dfrac{2}{5}}}7}}}{9}\Leftrightarrow y=\pm \dfrac{{{2.5}^{{{\log }_{\dfrac{2}{5}}}\sqrt{7}}}}{3}\approx \pm 0,121\in \left( -\ \dfrac{1}{5}\ ;\ \dfrac{1}{5} \right)$.
Trường hợp 2 : $m={{\log }_{\dfrac{2}{5}}}3$. Khi đó $\left( ** \right)$ trở thành $\dfrac{3{{t}^{2}}+10t+20}{{{t}^{2}}+2t+3}=3\Leftrightarrow 10t+20=6t+9\Leftrightarrow t=-\dfrac{11}{4}$.
Thay vào $\left( 2 \right)$ ta được ${{y}^{2}}=\dfrac{{{16.5}^{{{\log }_{\dfrac{2}{5}}}3}}}{81}\Leftrightarrow y=\pm \dfrac{{{4.5}^{{{\log }_{\dfrac{2}{5}}}\sqrt{3}}}}{9}\approx \pm 0,169\in \left( -\ \dfrac{1}{5}\ ;\ \dfrac{1}{5} \right)$.
Trường hợp 3: $m=-1$. Khi đó $\left( ** \right)$ có nghiệm duy nhất $t=-5$.
Thay vào $\left( 2 \right)$ ta được ${{y}^{2}}=\dfrac{1}{90}\Leftrightarrow y=\pm \dfrac{1}{3\sqrt{10}}\approx \pm 0,105\in \left( -\ \dfrac{1}{5}\ ;\ \dfrac{1}{5} \right)$.
Vậy có 6 số thực $y$ thỏa đề.
& 3{{x}^{2}}+10xy+20{{y}^{2}}>0 \\
& {{x}^{2}}+2xy+3{{y}^{2}}>0 \\
\end{aligned} \right.$.
Đặt ${{\log }_{2}}\left( 3{{x}^{2}}+10xy+20{{y}^{2}} \right)={{\log }_{5}}\left( {{x}^{2}}+2xy+3{{y}^{2}} \right)=m$. Ta có hệ
$\left\{ \begin{aligned}
& 3{{x}^{2}}+10xy+20{{y}^{2}}={{2}^{m}} \\
& {{x}^{2}}+2xy+3{{y}^{2}}={{5}^{m}} \\
\end{aligned} \right.\quad \left( * \right)$
Nếu $y=0$ thì $\left\{ \begin{aligned}
& 3{{x}^{2}}={{2}^{m}} \\
& {{x}^{2}}={{5}^{m}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& {{x}^{2}}={{5}^{m}} \\
& {{3.5}^{m}}={{2}^{m}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& m={{\log }_{\dfrac{2}{5}}}3 \\
& x=\pm \sqrt{{{5}^{{{\log }_{\dfrac{2}{5}}}3}}} \\
\end{aligned} \right. $. Suy ra có hai số thực $ x$ thỏa mãn.
Nếu $y\ne 0$ thì đặt $x=ty,\ \left( t\in \mathbb{R} \right)$. Hệ trên trở thành $\left\{ \begin{aligned}
& {{y}^{2}}\left( 3{{t}^{2}}+10t+20 \right)={{2}^{m}}\quad \left( 1 \right) \\
& {{y}^{2}}\left( {{t}^{2}}+2t+3 \right)={{5}^{m}}\quad \quad \ \left( 2 \right) \\
\end{aligned} \right.$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $\dfrac{3{{t}^{2}}+10t+20}{{{t}^{2}}+2t+3}={{\left( \dfrac{2}{5} \right)}^{m}}\quad \left( ** \right)$
Từ cách đặt suy ra ứng mỗi $y$ có duy nhất số thực $x$ khi và chỉ khi $\left( ** \right)$ có nghiệm duy nhất.
Xét hàm số $f\left( t \right)=\dfrac{3{{t}^{2}}+10t+20}{{{t}^{2}}+2t+3}$. Ta có ${f}'\left( t \right)=\dfrac{-2\left( 2{{t}^{2}}+11t+5 \right)}{{{\left( {{t}^{2}}+2t+3 \right)}^{2}}};$ ${f}'\left( t \right)=0\Leftrightarrow \left[ \begin{aligned}
& t=-5 \\
& t=-\ \dfrac{1}{2} \\
\end{aligned} \right.$.
Bảng biến thiên:
& {{\left( \dfrac{2}{5} \right)}^{m}}=7 \\
& {{\left( \dfrac{2}{5} \right)}^{m}}=3 \\
& {{\left( \dfrac{2}{5} \right)}^{m}}=\dfrac{5}{2} \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& m={{\log }_{\dfrac{2}{5}}}7 \\
& m={{\log }_{\dfrac{2}{5}}}3 \\
& m=-1 \\
\end{aligned} \right.$
Trường hợp 1 : $m={{\log }_{\dfrac{2}{5}}}7$. Khi đó $\left( ** \right)$ có nghiệm duy nhất $t=-\ \dfrac{1}{2}$.
Thay vào $\left( 2 \right)$ ta được ${{y}^{2}}=\dfrac{{{4.5}^{{{\log }_{\dfrac{2}{5}}}7}}}{9}\Leftrightarrow y=\pm \dfrac{{{2.5}^{{{\log }_{\dfrac{2}{5}}}\sqrt{7}}}}{3}\approx \pm 0,121\in \left( -\ \dfrac{1}{5}\ ;\ \dfrac{1}{5} \right)$.
Trường hợp 2 : $m={{\log }_{\dfrac{2}{5}}}3$. Khi đó $\left( ** \right)$ trở thành $\dfrac{3{{t}^{2}}+10t+20}{{{t}^{2}}+2t+3}=3\Leftrightarrow 10t+20=6t+9\Leftrightarrow t=-\dfrac{11}{4}$.
Thay vào $\left( 2 \right)$ ta được ${{y}^{2}}=\dfrac{{{16.5}^{{{\log }_{\dfrac{2}{5}}}3}}}{81}\Leftrightarrow y=\pm \dfrac{{{4.5}^{{{\log }_{\dfrac{2}{5}}}\sqrt{3}}}}{9}\approx \pm 0,169\in \left( -\ \dfrac{1}{5}\ ;\ \dfrac{1}{5} \right)$.
Trường hợp 3: $m=-1$. Khi đó $\left( ** \right)$ có nghiệm duy nhất $t=-5$.
Thay vào $\left( 2 \right)$ ta được ${{y}^{2}}=\dfrac{1}{90}\Leftrightarrow y=\pm \dfrac{1}{3\sqrt{10}}\approx \pm 0,105\in \left( -\ \dfrac{1}{5}\ ;\ \dfrac{1}{5} \right)$.
Vậy có 6 số thực $y$ thỏa đề.
Đáp án C.