Có bao nhiêu số nguyên $m\in \left( 0; 2023 \right)$ để phương...

+ Nhận định phương trình luôn có ít nhất 2 nghiệm phân biệt.
Xét hàm $g\left( x \right)={{2}^{x+1}}-\dfrac{3}{2}{{x}^{2}}-8-m$
Ta có: $\underset{x\to +\infty }{\mathop{\lim }} y=+\infty $ và $y\left( 0 \right)=-6-m<0$ với $m>0$
Từ đó suy ra phương trình $g\left( x \right)=0$ có ít nhất 1 nghiệm dương.
Vì $g\left( x \right)$ là hàm số chẵn nên phương trình ban đầu có ít nhất 2 nghiệm.
+ Xét hàm số $f\left( x \right)={{2}^{x+1}}-8$ trên $\mathbb{R}$. Từ đó ta suy ra đồ thị của hàm số $y=\left| f\left( \left| x \right| \right) \right|$
Ta có: ${f}'\left( x \right)={{2}^{x}}.\ln 4>0, \forall x$.
Xét hàm số $h\left( x \right)=\dfrac{3}{2}{{x}^{2}}$ trên $\mathbb{R}$. Từ đó tịnh tiến đồ thị $h\left( x \right)$ lên trên $m \left( m>0 \right)$ đơn vị theo phương của trục $Oy$ ta được đồ thị $y=\dfrac{3}{2}{{x}^{2}}+m$.
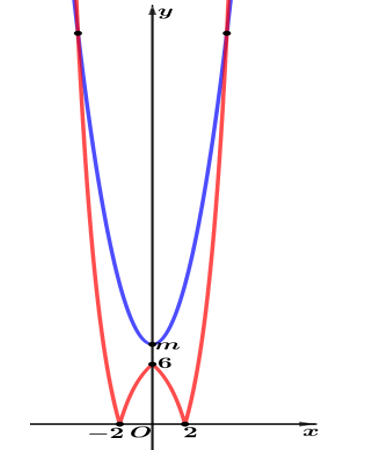Từ đồ thị, ta nhận thấy:
+ $0<m<6$ thì phương trình có 4 nghiệm phân biệt.
+ $m=6$ thì phương trình có 3 nghiệm phân biệt.
+ $m>6$ thì phương trình có 2 nghiệm phân biệt.
Kết hợp với $m\in \mathbb{Z}$ và $m\in \left( 0; 2023 \right)$ $\Rightarrow m=\left\{ 7; 8; 9;........;2022 \right\}$