Cho ${{z}_{1}},{{z}_{2}}$ là hai số phức thoả mãn $\left|...

Đặt ${{z}_{1}}=x+yi \left( x,y\in \mathbb{R} \right)$, ta có:
$\begin{aligned}
& \left| {{z}_{1}}+2 \right|=\left| {{z}_{1}}+2i \right| \\
& \Rightarrow \left| x+2+yi \right|=\left| x+\left( y+2 \right)i \right| \\
& \Rightarrow \sqrt{{{\left( x+2 \right)}^{2}}+{{y}^{2}}}=\sqrt{{{x}^{2}}+{{\left( y+2 \right)}^{2}}} \\
& \Leftrightarrow {{x}^{2}}+4x+4+{{y}^{2}}={{x}^{2}}+{{y}^{2}}+4y+4 \\
& \Leftrightarrow x=y \\
\end{aligned}$
Vậy tập hợp số phức thoả mãn là đường phân giác của góc phần tư thứ I $x=y$
Tương tự với ${{z}_{2}}$, ta có:
$\left| {{z}_{2}}+2+i \right|=\left| {{z}_{2}}-1+2i \right|$
$\begin{aligned}
& \Rightarrow \left| x+2+\left( y+1 \right)i \right|=\left| x-1+\left( y+2 \right)i \right| \\
& \Rightarrow \sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}} \\
& \Leftrightarrow y=3x \\
\end{aligned}$
Vậy tập hợp số phức thoả mãn là đường thẳng $y=3x$
Ta có hình vẽ mô tả như sau:
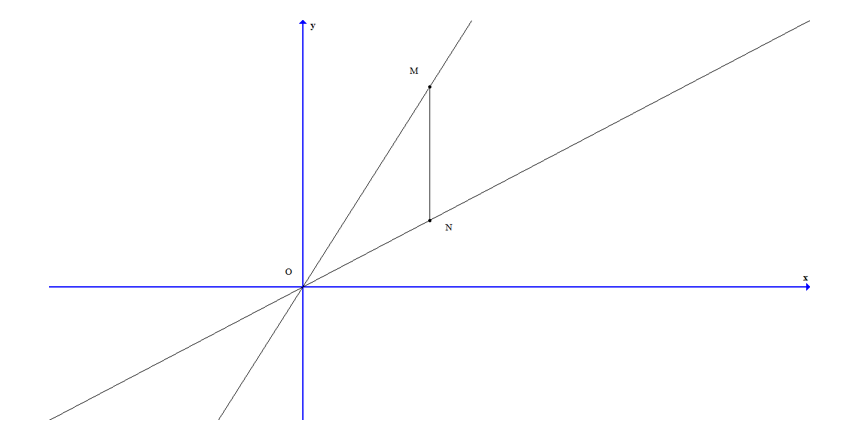$\cos \left( OM,ON \right)=\dfrac{\left| \overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}} \right|}{\left| \overrightarrow{{{n}_{1}}} \right|\left| \overrightarrow{{{n}_{2}}} \right|}=\dfrac{2}{\sqrt{5}}$
Theo định lý hàm cos cho tam giác OMN, ta được:
$\begin{aligned}
& M{{N}^{2}}=O{{M}^{2}}+O{{N}^{2}}-2OM.ON.\cos \left( OM,ON \right) \\
& \Rightarrow 45=O{{M}^{2}}+O{{N}^{2}}-\dfrac{4}{\sqrt{5}}OM.ON \\
& \Rightarrow O{{N}^{2}}-\dfrac{4}{\sqrt{5}}OM.ON+O{{M}^{2}}-45=0 \\
\end{aligned}$
Tính đenta cho phương trình ẩn $ON$, ta được:
$\begin{aligned}
& \Delta '={{\left( \dfrac{2}{\sqrt{5}}OM \right)}^{2}}-\left( O{{M}^{2}}-45 \right)=-\dfrac{1}{5}O{{M}^{2}}+45\ge 0 \\
& \Rightarrow O{{M}^{2}}\le 225 \\
& \Rightarrow 0\le OM\le 15 \\
\end{aligned}$
Vậy $O{{M}_{\max }}=15\to ON=6\sqrt{5}$
Vậy $\left| {{z}_{1}} \right|=6\sqrt{5}$