Google
Câu hỏi: Cho tứ diện $ABCD$ có $AC=BD=2a$. Gọi $H, K$ lần lượt là hình chiếu vuông góc của $A$ và $B$ lên đường thẳng $CD$. Biết $\overrightarrow{HC}=\overrightarrow{CD}=\overrightarrow{DK}$ ; góc giữa $AH$ và $BK$ bằng $60{}^\circ $. Thể tích khối tứ diện $ABCD$ bằng
A. $\dfrac{\sqrt{3}{{a}^{3}}}{6}$.
B. $\dfrac{\sqrt{3}{{a}^{3}}}{3}$.
C. $\dfrac{\sqrt{3}{{a}^{3}}}{4}$.
D. $\dfrac{\sqrt{3}{{a}^{3}}}{8}$
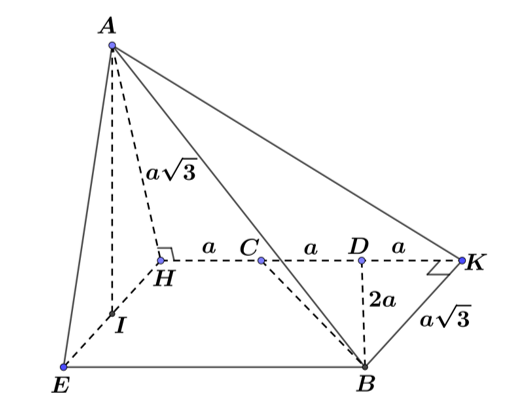Ta có: $AH=BK=\sqrt{{{\left( 2a \right)}^{2}}-a}=a\sqrt{3}$ (Định lý Pytago).
Dựng hình chữ nhật $HKBE$, ta có $HE=BK=a\sqrt{3}$ và $HE\parallel BK$.
Suy ra $\left( AH, BK \right)=\left( AH, HE \right)$.
Ta lại có : $\left\{ \begin{aligned}
& HK\bot AH \\
& HK\bot HE \\
\end{aligned} \right.\Rightarrow HK\bot \left( AHE \right) $, mà $ HK\subset \left( HKBE \right) $ $ \Rightarrow \left( AHE \right)\bot \left( HKBE \right)$.
Trường hợp 1: $\widehat{AHE}=60{}^\circ $. Khi đó tam giác $AHE$ đều. Suy ra hình chiếu vuông góc của $A$ trên $\left( HKBE \right)$ là trung điểm $I$ của $HE$ suy ra $AI=a\sqrt{3} . \dfrac{\sqrt{3}}{2}=\dfrac{3}{2}a$.
${{V}_{ABCD}}=\dfrac{1}{3} . AI .{{S}_{BCD}}=\dfrac{1}{3} . AI . \left( \dfrac{1}{2}BK.CD \right)=\dfrac{1}{3} . \dfrac{3}{2}a .\left( \dfrac{1}{2} . a\sqrt{3} . a \right)=\dfrac{{{a}^{3}}\sqrt{3}}{4}$ (đvtt).
Trường hợp 2: $\widehat{AHE}=120{}^\circ $. Khi đó ${{S}_{AHE}}=\dfrac{1}{2}AH.HE.\sin 120{}^\circ =\dfrac{1}{2}a\sqrt{3}. a\sqrt{3}. \dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}{{a}^{2}}}{4}$ (đvdt) suy ra $d\left( A , HE \right)=d\left( A , \left( HKBE \right) \right)=\dfrac{2{{S}_{AHE}}}{HE}=\dfrac{2.\dfrac{3\sqrt{3}{{a}^{2}}}{4}}{a\sqrt{3}}=\dfrac{3}{2}a$.
Thể tích khối tứ diện là: ${{V}_{ABCD}}=\dfrac{1}{3} . d\left( A , \left( HKBE \right) \right) .{{S}_{BCD}}=\dfrac{1}{3} . d\left( A , \left( HKBE \right) \right) . \left( \dfrac{1}{2}BK.CD \right)$
$=\dfrac{1}{3} . \dfrac{3}{2}a .\left( \dfrac{1}{2} . a\sqrt{3} . a \right)=\dfrac{{{a}^{3}}\sqrt{3}}{4}$ (đvtt).
A. $\dfrac{\sqrt{3}{{a}^{3}}}{6}$.
B. $\dfrac{\sqrt{3}{{a}^{3}}}{3}$.
C. $\dfrac{\sqrt{3}{{a}^{3}}}{4}$.
D. $\dfrac{\sqrt{3}{{a}^{3}}}{8}$
Dựng hình chữ nhật $HKBE$, ta có $HE=BK=a\sqrt{3}$ và $HE\parallel BK$.
Suy ra $\left( AH, BK \right)=\left( AH, HE \right)$.
Ta lại có : $\left\{ \begin{aligned}
& HK\bot AH \\
& HK\bot HE \\
\end{aligned} \right.\Rightarrow HK\bot \left( AHE \right) $, mà $ HK\subset \left( HKBE \right) $ $ \Rightarrow \left( AHE \right)\bot \left( HKBE \right)$.
Trường hợp 1: $\widehat{AHE}=60{}^\circ $. Khi đó tam giác $AHE$ đều. Suy ra hình chiếu vuông góc của $A$ trên $\left( HKBE \right)$ là trung điểm $I$ của $HE$ suy ra $AI=a\sqrt{3} . \dfrac{\sqrt{3}}{2}=\dfrac{3}{2}a$.
${{V}_{ABCD}}=\dfrac{1}{3} . AI .{{S}_{BCD}}=\dfrac{1}{3} . AI . \left( \dfrac{1}{2}BK.CD \right)=\dfrac{1}{3} . \dfrac{3}{2}a .\left( \dfrac{1}{2} . a\sqrt{3} . a \right)=\dfrac{{{a}^{3}}\sqrt{3}}{4}$ (đvtt).
Trường hợp 2: $\widehat{AHE}=120{}^\circ $. Khi đó ${{S}_{AHE}}=\dfrac{1}{2}AH.HE.\sin 120{}^\circ =\dfrac{1}{2}a\sqrt{3}. a\sqrt{3}. \dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}{{a}^{2}}}{4}$ (đvdt) suy ra $d\left( A , HE \right)=d\left( A , \left( HKBE \right) \right)=\dfrac{2{{S}_{AHE}}}{HE}=\dfrac{2.\dfrac{3\sqrt{3}{{a}^{2}}}{4}}{a\sqrt{3}}=\dfrac{3}{2}a$.
Thể tích khối tứ diện là: ${{V}_{ABCD}}=\dfrac{1}{3} . d\left( A , \left( HKBE \right) \right) .{{S}_{BCD}}=\dfrac{1}{3} . d\left( A , \left( HKBE \right) \right) . \left( \dfrac{1}{2}BK.CD \right)$
$=\dfrac{1}{3} . \dfrac{3}{2}a .\left( \dfrac{1}{2} . a\sqrt{3} . a \right)=\dfrac{{{a}^{3}}\sqrt{3}}{4}$ (đvtt).
Đáp án C.
