Cho hình phẳng được giới hạn bởi các đường $y=\sqrt{4-x^2}, y=2...

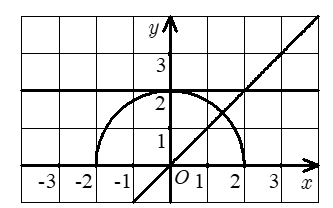Các phương trình hoành độ giao điểm:
$
\begin{aligned}
& * \sqrt{4-x^2}=x \Leftrightarrow\left\{\begin{array} { l }
{ x \geq 0 } \\
{ 4 - x ^ { 2 } = x ^ { 2 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
x=\sqrt{2}
\end{array}\right.\right. \\
& * \sqrt{4-x^2}=2 \Leftrightarrow x=0 \\
& * x=2
\end{aligned}
$
Diện tích cần tính là: $S=\int_0^{\sqrt{2}}\left(2-\sqrt{4-x^2}\right) \mathrm{d} x+\int_{\sqrt{2}}^2(2-x) \mathrm{d} x=\int_0^{\sqrt{2}} 2 \mathrm{~d} x+\int_{\sqrt{2}}^2(2-x) \mathrm{d} x-$
$
\begin{aligned}
& \int_0^{\sqrt{2}} \sqrt{4-x^2} \mathrm{~d} x \\
& =\left.(2 x)\right|_0 ^{\sqrt{2}}+\left.\left(2 x-\dfrac{x^2}{2}\right)\right|_{\sqrt{2}} ^2-\int_0^{\sqrt{2}} \sqrt{4-x^2} \mathrm{~d} x=2 \sqrt{2}+3-2 \sqrt{2}-\int_0^{\sqrt{2}} \sqrt{4-x^2} \mathrm{~d} x=3- \\
& \int_0^{\sqrt{2}} \sqrt{4-x^2} \mathrm{~d} x
\end{aligned}
$
Đặt $x=2 \sin t \Rightarrow \mathrm{d} x=2 \cos t \mathrm{~d} t$. Đổi cận: $x=0 \Rightarrow t=0 ; x=\sqrt{2} \Rightarrow t=\dfrac{\pi}{4}$.
Ta có $\int_0^{\sqrt{2}} \sqrt{4-x^2} \mathrm{~d} x=\int_0^{\dfrac{\pi}{4}} \sqrt{4-4 \sin ^2 t} \cdot 2 \cos t \mathrm{~d} x=\int_0^{\dfrac{\pi}{4}} 4 \cos ^2 t \mathrm{~d} x=\int_0^{\dfrac{\pi}{4}} 2(1+\cos 2 t) \mathrm{d} x$ $=\left.2\left(t+\dfrac{1}{2} \sin 2 t\right)\right|_0 ^{\dfrac{\pi}{4}}=2\left(\dfrac{\pi}{4}+\dfrac{1}{2}\right)=\dfrac{\pi}{2}+1$
Vậy $S=3-\dfrac{\pi}{2}-1=2-\dfrac{1}{2} \cdot \pi$.
Theo kí hiệu của bài toán ta suy ra $a=2, b=-\dfrac{1}{2}$. Do đó mệnh đề đúng là $a^2+4 b^2 \geq 5$.