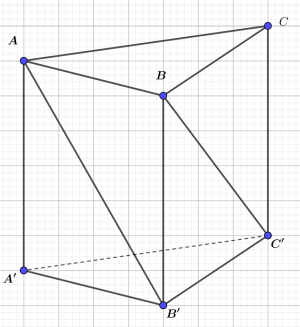
Câu hỏi: Cho hình lăng trụ tam giác đều $ABC.{A}'{B}'{C}'$ có cạnh đáy bằng $2a$, góc giữa hai đường thẳng $A{B}'$ và $B{C}'$ bằng ${{60}^{0}}$ ( tham khảo hình bên dưới). Tính thể tích $V$ khối lăng trụ đó.
A. $V=\dfrac{2\sqrt{6}{{a}^{3}}}{3}$.
B. $V=2\sqrt{6}{{a}^{3}}$.
C. $V=\dfrac{2\sqrt{3}{{a}^{3}}}{3}$.
D. $V=2\sqrt{3}{{a}^{3}}$.
$\text{IJ=I}K=\dfrac{1}{2}AB'=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}$
+) Gọi $I,J,K$ lần lượt là trung điểm của $BB',B'C',AB$. Khi đó, ta có:
$\text{IJ}//BC,IK//AB'$
Suy ra: $\left( A{B}',B{C}' \right)=\left( IJ,IK \right)$. Gọi H là trung điểm của ${A}'{B}'$.
TH1: $\left( IJ,IK \right)=\widehat{JIK}={{60}^{0}}$
Khi đó $\Delta IJK$ đều và $KJ=IJ=IK=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}$
Mà $KJ=\sqrt{K{{H}^{2}}+H{{J}^{2}}}=\sqrt{{{x}^{2}}+{{a}^{2}}}$.
Ta có phương trình: $\sqrt{{{x}^{2}}+{{a}^{2}}}=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}\Leftrightarrow 3x{}^{2}=0\Leftrightarrow x=0$ (mâu thuẫn với đ/k: $A{A}'=x>0$ )
Suy ra trường hợp này không xảy ra.
TH2: $\left( IJ,IK \right)={{180}^{0}}-\widehat{JIK}={{60}^{0}}\Rightarrow \widehat{JIK}={{120}^{0}}$
Khi đó $\Delta IJK$ cân tại $I$ có $IJ=IK=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}$ và $\widehat{JIK}={{120}^{0}}$.
Suy ra: $K{{J}^{2}}=I{{J}^{2}}+I{{K}^{2}}-2IJ.IK.\cos {{120}^{0}}=3I{{J}^{2}}=\dfrac{3}{4}\left( {{x}^{2}}+4{{a}^{2}} \right)$
Mà $K{{J}^{2}}=K{{H}^{2}}+H{{J}^{2}}={{x}^{2}}+{{a}^{2}}$.
Ta có phương trình: ${{x}^{2}}+{{a}^{2}}=\dfrac{3}{4}\left( {{x}^{2}}+4{{a}^{2}} \right)\Leftrightarrow {{x}^{2}}=8{{a}^{2}}\Leftrightarrow x=2a\sqrt{2}$
Suy ra: $V=A{A}'.{{S}_{ABC}}=2a\sqrt{2}.{{a}^{2}}\sqrt{3}=2\sqrt{6}{{a}^{3}}$.
A. $V=\dfrac{2\sqrt{6}{{a}^{3}}}{3}$.
B. $V=2\sqrt{6}{{a}^{3}}$.
C. $V=\dfrac{2\sqrt{3}{{a}^{3}}}{3}$.
D. $V=2\sqrt{3}{{a}^{3}}$.
i
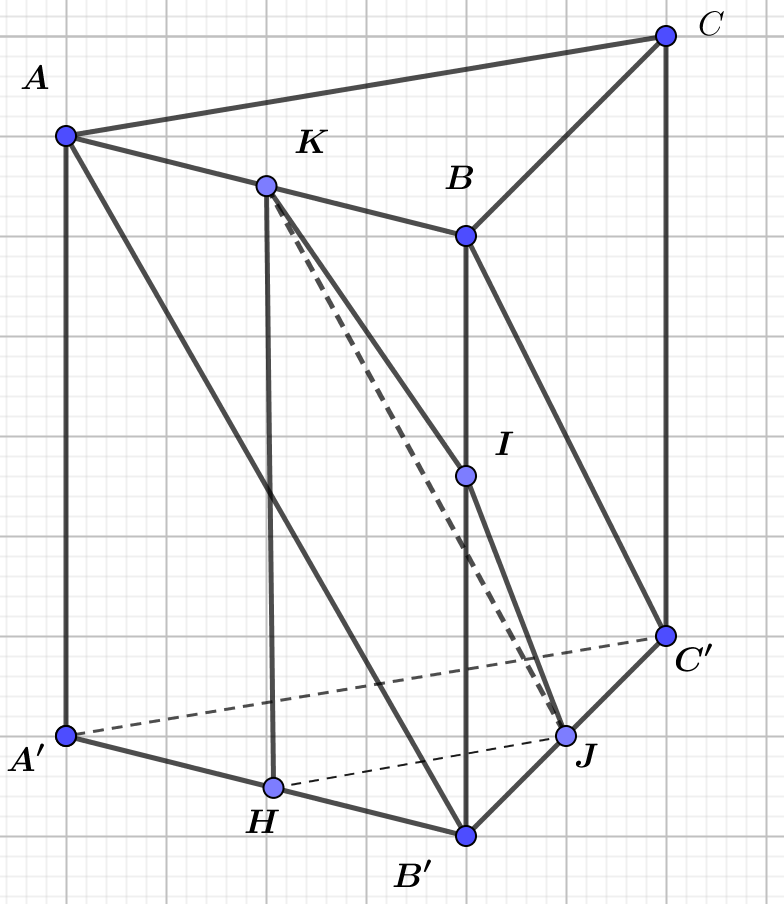
+) Ta có: $V=\text{AA }\!\!'\!\!\text{.}{{\text{S}}_{ABC}}$ Đặt $\text{AA }\!\!'\!\!\text{ =x0}$. Dễ thấy $\Delta \text{IJ}K$ $\text{IJ=I}K=\dfrac{1}{2}AB'=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}$
+) Gọi $I,J,K$ lần lượt là trung điểm của $BB',B'C',AB$. Khi đó, ta có:
$\text{IJ}//BC,IK//AB'$
Suy ra: $\left( A{B}',B{C}' \right)=\left( IJ,IK \right)$. Gọi H là trung điểm của ${A}'{B}'$.
TH1: $\left( IJ,IK \right)=\widehat{JIK}={{60}^{0}}$
Khi đó $\Delta IJK$ đều và $KJ=IJ=IK=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}$
Mà $KJ=\sqrt{K{{H}^{2}}+H{{J}^{2}}}=\sqrt{{{x}^{2}}+{{a}^{2}}}$.
Ta có phương trình: $\sqrt{{{x}^{2}}+{{a}^{2}}}=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}\Leftrightarrow 3x{}^{2}=0\Leftrightarrow x=0$ (mâu thuẫn với đ/k: $A{A}'=x>0$ )
Suy ra trường hợp này không xảy ra.
TH2: $\left( IJ,IK \right)={{180}^{0}}-\widehat{JIK}={{60}^{0}}\Rightarrow \widehat{JIK}={{120}^{0}}$
Khi đó $\Delta IJK$ cân tại $I$ có $IJ=IK=\dfrac{1}{2}\sqrt{{{x}^{2}}+4{{a}^{2}}}$ và $\widehat{JIK}={{120}^{0}}$.
Suy ra: $K{{J}^{2}}=I{{J}^{2}}+I{{K}^{2}}-2IJ.IK.\cos {{120}^{0}}=3I{{J}^{2}}=\dfrac{3}{4}\left( {{x}^{2}}+4{{a}^{2}} \right)$
Mà $K{{J}^{2}}=K{{H}^{2}}+H{{J}^{2}}={{x}^{2}}+{{a}^{2}}$.
Ta có phương trình: ${{x}^{2}}+{{a}^{2}}=\dfrac{3}{4}\left( {{x}^{2}}+4{{a}^{2}} \right)\Leftrightarrow {{x}^{2}}=8{{a}^{2}}\Leftrightarrow x=2a\sqrt{2}$
Suy ra: $V=A{A}'.{{S}_{ABC}}=2a\sqrt{2}.{{a}^{2}}\sqrt{3}=2\sqrt{6}{{a}^{3}}$.
Đáp án B.