Google
Câu hỏi: Cho hình chóp $S \cdot A B C D$ có đáy là hình vuông cạnh $2 a$, tam giác $S A B$ đều, góc giữa $(S C D)$ và $(A B C D)$ bằng $60^{\circ}$. Gọi $M$ là trung điểm của cạnh $A B$. Biết rằng hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $(A B C D)$ nằm trong hình vuông $A B C D$. Khoảng cách giữa hai đường thẳng $S M$ và $A C$ là
A. $\dfrac{a \sqrt{5}}{5}$.
B. $\dfrac{5 a \sqrt{3}}{3}$.
C. $\dfrac{a \sqrt{5}}{10}$.
D. $\dfrac{3 a \sqrt{5}}{10}$.
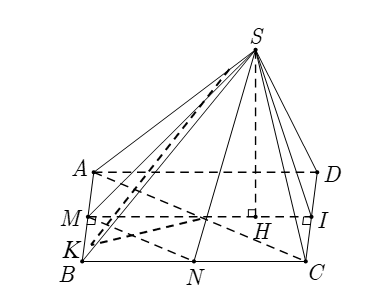Gọi $I$ là trung điểm cạnh $C D$, khi đó $\left\{\begin{array}{l}A B \perp S M \\ A B \perp M I\end{array} \Rightarrow A B \perp(S M I)\right.$.
Do $C D / / A B$ nên $C D \perp(S M I) \Rightarrow((S C D),(A B C D))=\widehat{S I M}$.
Vẽ $S H \perp M I$ tại $H \in M I$ thì $S H \perp(A B C D)$.
Tam giác $S M I$ có $S M^2=M I^2+S I^2-2 \cdot M I \cdot S I \cdot \cos \widehat{S I M} \Leftrightarrow 3 a^2=4 a^2+S I^2-2 a$.SI $\Leftrightarrow S I^2-2 a \cdot S I+a^2=0 \Leftrightarrow S I=a$.
Ta thấy $S M^2+S I^2=M I^2$ nên $\triangle S M I$ vuông tại $S$. Suy ra $S H=\dfrac{S M \cdot S I}{M I}=\dfrac{a \sqrt{3}}{2} ; H M=\dfrac{3 a}{2}$. Gọi $O=A C \cap B D ; N$ là trung điểm cạnh $B C$ ta có $A C / /(S M N)$.
Do đó, $d(A C, S M)=d(A C,(S M N))=d(O,(S M N))=\dfrac{2}{3} d(H,(S M N))$.
Gọi $K$ là hình chiếu của $H$ lên $M N$, ta có $\triangle H K M$ vuông cân tại $K$ nên $H K=\dfrac{H M}{\sqrt{2}}=\dfrac{3 a \sqrt{2}}{4}$.
Vậy $d(A C, S M)=\dfrac{2}{3} \cdot \dfrac{S H \cdot H K}{\sqrt{S H^2+H K^2}}=\dfrac{a \sqrt{5}}{5}$.
A. $\dfrac{a \sqrt{5}}{5}$.
B. $\dfrac{5 a \sqrt{3}}{3}$.
C. $\dfrac{a \sqrt{5}}{10}$.
D. $\dfrac{3 a \sqrt{5}}{10}$.
Do $C D / / A B$ nên $C D \perp(S M I) \Rightarrow((S C D),(A B C D))=\widehat{S I M}$.
Vẽ $S H \perp M I$ tại $H \in M I$ thì $S H \perp(A B C D)$.
Tam giác $S M I$ có $S M^2=M I^2+S I^2-2 \cdot M I \cdot S I \cdot \cos \widehat{S I M} \Leftrightarrow 3 a^2=4 a^2+S I^2-2 a$.SI $\Leftrightarrow S I^2-2 a \cdot S I+a^2=0 \Leftrightarrow S I=a$.
Ta thấy $S M^2+S I^2=M I^2$ nên $\triangle S M I$ vuông tại $S$. Suy ra $S H=\dfrac{S M \cdot S I}{M I}=\dfrac{a \sqrt{3}}{2} ; H M=\dfrac{3 a}{2}$. Gọi $O=A C \cap B D ; N$ là trung điểm cạnh $B C$ ta có $A C / /(S M N)$.
Do đó, $d(A C, S M)=d(A C,(S M N))=d(O,(S M N))=\dfrac{2}{3} d(H,(S M N))$.
Gọi $K$ là hình chiếu của $H$ lên $M N$, ta có $\triangle H K M$ vuông cân tại $K$ nên $H K=\dfrac{H M}{\sqrt{2}}=\dfrac{3 a \sqrt{2}}{4}$.
Vậy $d(A C, S M)=\dfrac{2}{3} \cdot \dfrac{S H \cdot H K}{\sqrt{S H^2+H K^2}}=\dfrac{a \sqrt{5}}{5}$.
Đáp án A.