Cho hình chóp $S . A B C D$ có $A B C D$ là hình vuông, $\triangle...

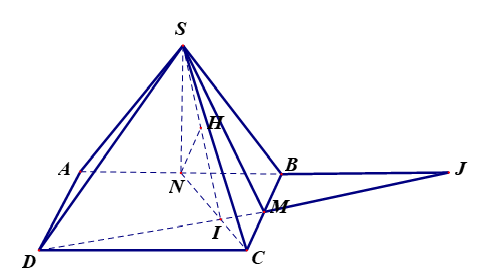$\begin{aligned} & \text { + Không mất tính tổng quát, đặt } A B=2 \text {. } \\ & + \text { Gọi } N \text { là trung điểm } A B \text { suy ra } S N \perp A B \Rightarrow S N \perp(A B C D) \text {. } \\ & + \text { Gọi } h=d(A,(S D M)) \Rightarrow \sin \alpha=\dfrac{h}{S A} . \\ & \text { Gọi } I=D M \cap C N, J=A B \cap D M . \\ & + \text { Ta có } \dfrac{d(A,(S D M))}{d(\mathrm{~N},(S D M))}=\dfrac{\mathrm{AJ}}{N J}=\dfrac{4}{3} \\ & \Rightarrow h=d(A,(S D M))=\dfrac{4}{3} d(\mathrm{~N},(S D M)) .\end{aligned}$
+ ta có $\Delta CNB=\Delta DMC\Rightarrow \widehat{NCB}=\widehat{MDC}$
$
\begin{aligned}
& \Rightarrow \widehat{N C B}+\widehat{D M C}=\widehat{M D C}+\widehat{D M C}=180^{\circ}-\widehat{M C D}=90^{\circ} \\
& \Rightarrow D M \perp C N \Rightarrow D M \perp(S N C) . \\
& + \text { Gọi } N H \text { là đường cao } \Delta S N I \Rightarrow N H \perp(S D M) \\
& \Rightarrow d(\mathrm{~N},(S D M))=N H . \\
& +\Delta N I J \text { đồng dạng } \Delta M B J \Rightarrow \dfrac{N I}{M B}=\dfrac{N J}{M J} \\
& \Rightarrow N I=\dfrac{N J}{M J} \cdot M B=\dfrac{N J}{\sqrt{M B^2+B J^2}} \cdot M B=\dfrac{3}{\sqrt{1^2+2^2}} \cdot 1=\dfrac{3}{\sqrt{5}} \\
& +\Delta S A B \text { là tam giác đều cạnh bằng } 2 \Rightarrow S N=\sqrt{3} \\
& +\dfrac{1}{N H^2}=\dfrac{1}{N S^2}+\dfrac{1}{N I^2} \Rightarrow N H=\dfrac{3 \sqrt{2}}{4} \\
& +h=d(A,(S D M))=\dfrac{4}{3} d(\mathrm{~N},(S D M))=\dfrac{4}{3} \cdot \dfrac{3 \sqrt{2}}{4}=\sqrt{2} \\
& \Rightarrow \sin \alpha=\dfrac{h}{S A}=\dfrac{\sqrt{2}}{2} \Rightarrow \alpha=45^{\circ} .
\end{aligned}
$