Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a$, $SA\bot \left( ABCD \right)$. Góc giữa hai mặt phẳng $\left( SBC \right)$ và $\left( SCD \right)$ bằng $\alpha $ với $\cos \alpha =\dfrac{9}{16}$. Thể tích của khối chóp $S.ABCD$ bằng:
A. $\dfrac{{{a}^{3}}\sqrt{7}}{3}$.
B. $\dfrac{{{a}^{3}}\sqrt{57}}{3}$.
C. $\dfrac{{{a}^{3}}\sqrt{57}}{9}$.
D. $\dfrac{{{a}^{3}}\sqrt{7}}{9}$.
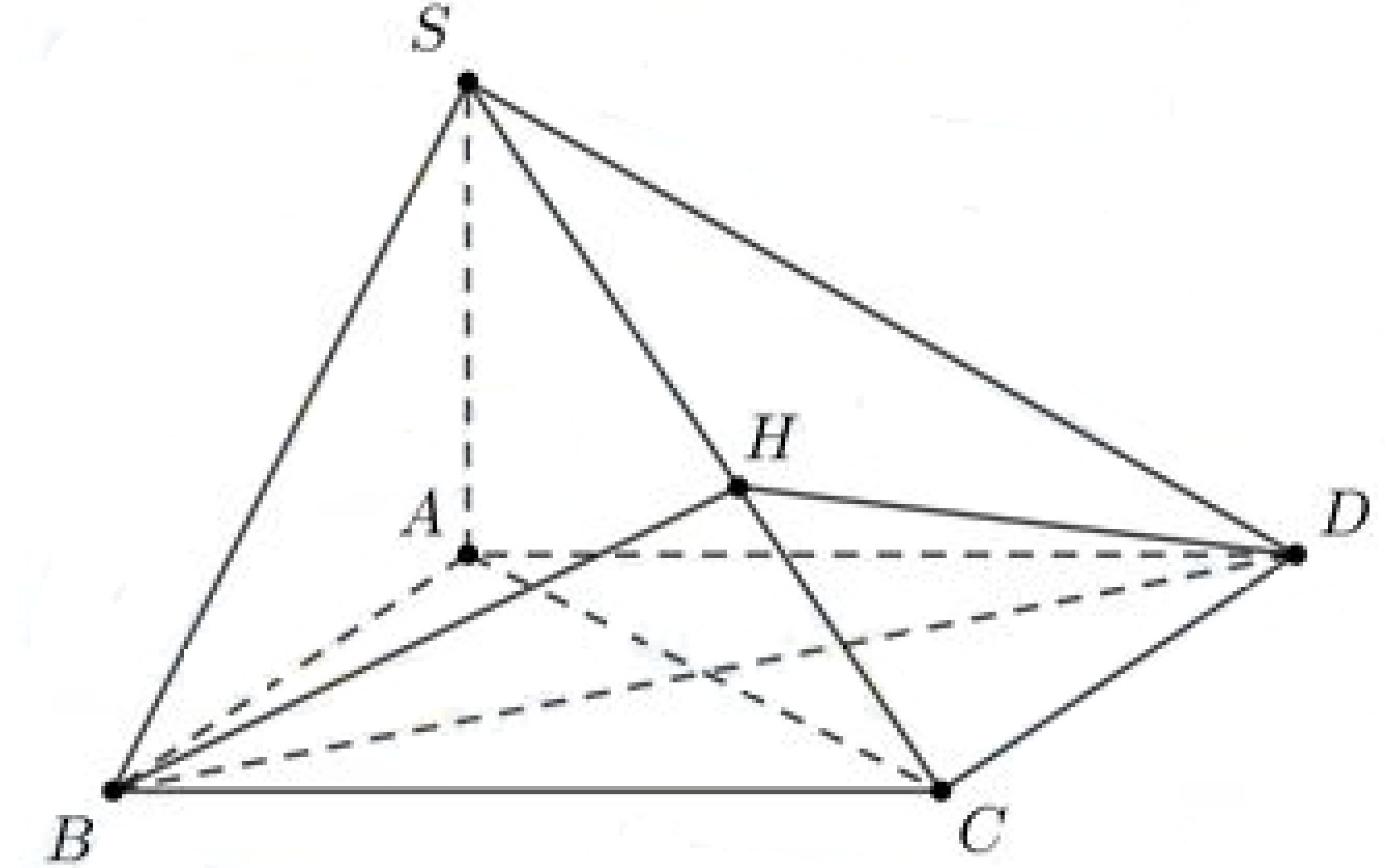Dựng $BH\bot SC$ $\Rightarrow SC\bot \left( BHD \right)\Rightarrow SC\bot DH$ $\Rightarrow \left( \left( SBC \right),\left( SCD \right) \right)=\left( BH,DH \right)$
TH1: $\cos \widehat{BHD}=-\dfrac{9}{16}$
Ta có:
$BD=AC\sqrt{2}=a\sqrt{2}$
$B{{D}^{2}}=B{{H}^{2}}+D{{H}^{2}}-2BH\cdot DH\cdot \cos \widehat{BHD}$
Mà $BH=DH\left( \Delta SBC=\Delta SDC \right)$
Nên $B{{D}^{2}}=B{{H}^{2}}+B{{H}^{2}}-2BH\cdot BH\cdot \dfrac{-9}{16}=\dfrac{25}{8}B{{H}^{2}}$ $\Rightarrow B{{H}^{2}}=\dfrac{8}{25}2{{a}^{2}}\Leftrightarrow BH=\dfrac{4}{5}a$
$\dfrac{1}{B{{H}^{2}}}=\dfrac{1}{S{{B}^{2}}}+\dfrac{1}{B{{C}^{2}}}\Leftrightarrow \dfrac{1}{S{{B}^{2}}}=\dfrac{1}{B{{H}^{2}}}-\dfrac{1}{B{{C}^{2}}}\Leftrightarrow SB=\dfrac{BH\cdot BC}{\sqrt{B{{C}^{2}}-B{{H}^{2}}}}=\dfrac{4}{3}a$
$SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=\dfrac{\sqrt{7}}{3}a$
$\Rightarrow {{V}_{S.ABCD}}=\dfrac{1}{3}SA\cdot AB\cdot AD=\dfrac{1}{3}\cdot \dfrac{\sqrt{7}}{3}a\cdot a\cdot a=\dfrac{\sqrt{7}}{9}{{a}^{3}}$
TH2: $\cos \widehat{BHD}=\dfrac{9}{16}$
Ta có: $B{{D}^{2}}=B{{H}^{2}}+D{{H}^{2}}-2BH\cdot DH\cdot \cos \widehat{BHD}=B{{H}^{2}}+B{{H}^{2}}-2BH\cdot BH\cdot \dfrac{9}{16}=\dfrac{7}{8}B{{H}^{2}}$
$\Rightarrow B{{H}^{2}}=\dfrac{8}{7}2{{a}^{2}}\Leftrightarrow BH=\dfrac{4\sqrt{7}}{7}a>BC$ (vô lý)
A. $\dfrac{{{a}^{3}}\sqrt{7}}{3}$.
B. $\dfrac{{{a}^{3}}\sqrt{57}}{3}$.
C. $\dfrac{{{a}^{3}}\sqrt{57}}{9}$.
D. $\dfrac{{{a}^{3}}\sqrt{7}}{9}$.
TH1: $\cos \widehat{BHD}=-\dfrac{9}{16}$
Ta có:
$BD=AC\sqrt{2}=a\sqrt{2}$
$B{{D}^{2}}=B{{H}^{2}}+D{{H}^{2}}-2BH\cdot DH\cdot \cos \widehat{BHD}$
Mà $BH=DH\left( \Delta SBC=\Delta SDC \right)$
Nên $B{{D}^{2}}=B{{H}^{2}}+B{{H}^{2}}-2BH\cdot BH\cdot \dfrac{-9}{16}=\dfrac{25}{8}B{{H}^{2}}$ $\Rightarrow B{{H}^{2}}=\dfrac{8}{25}2{{a}^{2}}\Leftrightarrow BH=\dfrac{4}{5}a$
$\dfrac{1}{B{{H}^{2}}}=\dfrac{1}{S{{B}^{2}}}+\dfrac{1}{B{{C}^{2}}}\Leftrightarrow \dfrac{1}{S{{B}^{2}}}=\dfrac{1}{B{{H}^{2}}}-\dfrac{1}{B{{C}^{2}}}\Leftrightarrow SB=\dfrac{BH\cdot BC}{\sqrt{B{{C}^{2}}-B{{H}^{2}}}}=\dfrac{4}{3}a$
$SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=\dfrac{\sqrt{7}}{3}a$
$\Rightarrow {{V}_{S.ABCD}}=\dfrac{1}{3}SA\cdot AB\cdot AD=\dfrac{1}{3}\cdot \dfrac{\sqrt{7}}{3}a\cdot a\cdot a=\dfrac{\sqrt{7}}{9}{{a}^{3}}$
TH2: $\cos \widehat{BHD}=\dfrac{9}{16}$
Ta có: $B{{D}^{2}}=B{{H}^{2}}+D{{H}^{2}}-2BH\cdot DH\cdot \cos \widehat{BHD}=B{{H}^{2}}+B{{H}^{2}}-2BH\cdot BH\cdot \dfrac{9}{16}=\dfrac{7}{8}B{{H}^{2}}$
$\Rightarrow B{{H}^{2}}=\dfrac{8}{7}2{{a}^{2}}\Leftrightarrow BH=\dfrac{4\sqrt{7}}{7}a>BC$ (vô lý)
Đáp án D.