Google
Câu hỏi: Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $a$. Gọi $M$ là trung điểm $BC$. Biết rằng góc giữa đường thẳng $DM$ với mặt bên $\left( SAB \right)$ là góc $\alpha $ thỏa mãn $\tan \alpha =\dfrac{\sqrt{26}}{13}$. Tính thể tích khối chóp $S.ABCD$.
A. $\dfrac{{{a}^{3}}\sqrt{2}}{6}$.
B. $\dfrac{4{{a}^{3}}}{9}$.
C. $\dfrac{{{a}^{3}}\sqrt{3}}{3}$.
D. $\dfrac{{{a}^{3}}\sqrt{6}}{3}$.
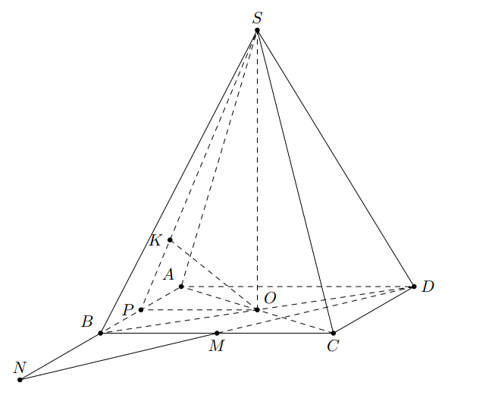Gọi $N$ là điểm đối xứng với $A$ qua $B$ ; $P$ là trung điểm của $AB$ ; $K$ là hình chiếu của $O$ lên cạnh $SP$.
Khi đó $DN=a\sqrt{5}; OP=\dfrac{a}{2}$.
Ta có $\tan \alpha =\dfrac{\sqrt{26}}{13}$ nên $\sin \alpha =\dfrac{\sqrt{30}}{15}$.
Do đó $\text{d}\left( D,\left( SAB \right) \right)=DN\cdot \sin \alpha =\dfrac{a\sqrt{6}}{3}$ nên $OK=\text{d}\left( O,\left( SAB \right) \right)=\dfrac{1}{2}\text{d}\left( D,\left( SAB \right) \right)=\dfrac{a\sqrt{6}}{6}$.
Mặt khác $\dfrac{1}{O{{K}^{2}}}=\dfrac{1}{O{{S}^{2}}}+\dfrac{1}{O{{P}^{2}}}$ suy ra $SO=\dfrac{a\sqrt{2}}{2}$.
Thể tích khối chóp $S.ABCD$ là $V=\dfrac{1}{3}\cdot A{{B}^{2}}\cdot SO=\dfrac{1}{3}\cdot {{a}^{2}}\cdot \dfrac{a\sqrt{2}}{2}=\dfrac{{{a}^{3}}\sqrt{2}}{6}$.
A. $\dfrac{{{a}^{3}}\sqrt{2}}{6}$.
B. $\dfrac{4{{a}^{3}}}{9}$.
C. $\dfrac{{{a}^{3}}\sqrt{3}}{3}$.
D. $\dfrac{{{a}^{3}}\sqrt{6}}{3}$.
Khi đó $DN=a\sqrt{5}; OP=\dfrac{a}{2}$.
Ta có $\tan \alpha =\dfrac{\sqrt{26}}{13}$ nên $\sin \alpha =\dfrac{\sqrt{30}}{15}$.
Do đó $\text{d}\left( D,\left( SAB \right) \right)=DN\cdot \sin \alpha =\dfrac{a\sqrt{6}}{3}$ nên $OK=\text{d}\left( O,\left( SAB \right) \right)=\dfrac{1}{2}\text{d}\left( D,\left( SAB \right) \right)=\dfrac{a\sqrt{6}}{6}$.
Mặt khác $\dfrac{1}{O{{K}^{2}}}=\dfrac{1}{O{{S}^{2}}}+\dfrac{1}{O{{P}^{2}}}$ suy ra $SO=\dfrac{a\sqrt{2}}{2}$.
Thể tích khối chóp $S.ABCD$ là $V=\dfrac{1}{3}\cdot A{{B}^{2}}\cdot SO=\dfrac{1}{3}\cdot {{a}^{2}}\cdot \dfrac{a\sqrt{2}}{2}=\dfrac{{{a}^{3}}\sqrt{2}}{6}$.
Đáp án A.
