Google
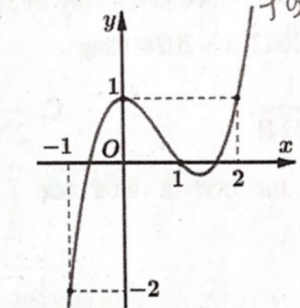
Câu hỏi: Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và $f(0)\ge -1$.Đồ thị của hàm số $y=f'(x)$ như hình vẽ.
Hàm sô $y=\left| f(x)-\dfrac{{{x}^{3}}}{3}+{{x}^{2}}-x+2 \right|$ có giá trị nhỏ nhất là $m\in \left( 0;1 \right)$ khi và chỉ khi
A. $f(2)<-\dfrac{1}{3}$
B. $f(2)\le -\dfrac{1}{3}$
C. $f(2)\ge -\dfrac{4}{3}$
D. $f(2)>-\dfrac{4}{3}$
A. $f(2)<-\dfrac{1}{3}$
B. $f(2)\le -\dfrac{1}{3}$
C. $f(2)\ge -\dfrac{4}{3}$
D. $f(2)>-\dfrac{4}{3}$
Xét $g(x)=f(x)-\dfrac{{{x}^{3}}}{3}+{{x}^{2}}-x+2\Rightarrow g'(x)=f'(x)-{{x}^{2}}+2x-1; g'(x)=0\Leftrightarrow f'(x)={{x}^{2}}-2x+1$.
Vẽ $\left( P \right):y={{x}^{2}}-2x+1$ cắt $y=f'(x)$ tại ba điểm có hoành độ $x=0;x=1;x=2$.
Ta có bảng biến thiên của $y=g(x)$ như sau
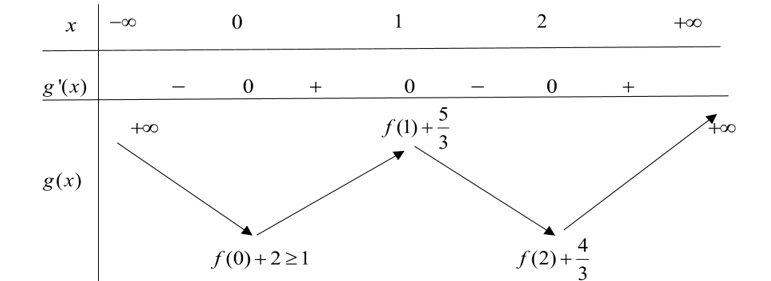Từ bảng biến thiên ta thấy:
Nếu $f(2)+\dfrac{4}{3}<0\Rightarrow \left| g(x) \right|\ge 0\Rightarrow Min\left| g(x) \right|=0$.
Do đó để $Min\left| g(x) \right|=m\in \left( 0;1 \right)\Rightarrow \left\{ \begin{matrix}
f(2)+\dfrac{4}{3}>0 \\
f(2)+\dfrac{4}{3}<1 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
f(2)>\dfrac{-4}{3} \\
f(2)<-\dfrac{1}{3} \\
\end{matrix} \right.$.
Vậy $-\dfrac{4}{3}<f(2)<\dfrac{-1}{3}$
Vẽ $\left( P \right):y={{x}^{2}}-2x+1$ cắt $y=f'(x)$ tại ba điểm có hoành độ $x=0;x=1;x=2$.
Ta có bảng biến thiên của $y=g(x)$ như sau
Nếu $f(2)+\dfrac{4}{3}<0\Rightarrow \left| g(x) \right|\ge 0\Rightarrow Min\left| g(x) \right|=0$.
Do đó để $Min\left| g(x) \right|=m\in \left( 0;1 \right)\Rightarrow \left\{ \begin{matrix}
f(2)+\dfrac{4}{3}>0 \\
f(2)+\dfrac{4}{3}<1 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
f(2)>\dfrac{-4}{3} \\
f(2)<-\dfrac{1}{3} \\
\end{matrix} \right.$.
Vậy $-\dfrac{4}{3}<f(2)<\dfrac{-1}{3}$
Đáp án A.
