Google
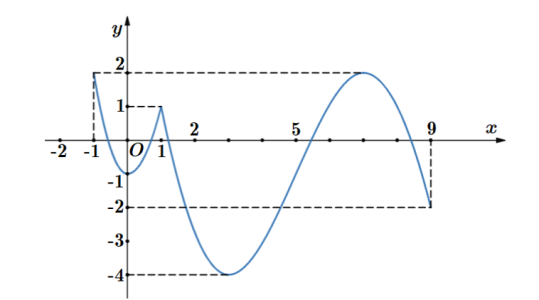
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục trên $\left[ -1;9 \right]$ và có đồ thị là đường cong trong hình vẽ dưới đây
Có bao nhiêu giá trị nguyên của tham số $m$ để bất phương trình ${{16.3}^{f\left( x \right)}}-\left[ {{f}^{2}}\left( x \right)+2f\left( x \right)-8 \right]{{4}^{f\left( x \right)}}\ge \left( {{m}^{2}}-3m \right){{6}^{f\left( x \right)}}$ có nghiệm đúng với mọi giá trị thuộc $\left[ -1;9 \right]$.
A. $6$.
B. $32$.
C. $5$.
D. $31$.
A. $6$.
B. $32$.
C. $5$.
D. $31$.
${{16.3}^{f\left( x \right)}}-\left[ {{f}^{2}}\left( x \right)+2f\left( x \right)-8 \right]{{4}^{f\left( x \right)}}\ge \left( {{m}^{2}}-3m \right){{6}^{f\left( x \right)}}$
$\Leftrightarrow 16{{\left( \dfrac{1}{2} \right)}^{f\left( x \right)}}-\left[ {{f}^{2}}\left( x \right)+2f\left( x \right)-8 \right]{{\left( \dfrac{2}{3} \right)}^{f\left( x \right)}}\ge {{m}^{2}}-3m$
Đặt $t=f\left( x \right)$, từ đồ thị ta thấy được $-4\le f\left( x \right)\le 2$ $\Rightarrow t\in \left[ -4;2 \right]$.
Để ${{16.3}^{f\left( x \right)}}-\left[ {{f}^{2}}\left( x \right)+2f\left( x \right)-8 \right]{{4}^{f\left( x \right)}}\ge \left( {{m}^{2}}-3m \right){{6}^{f\left( x \right)}}$ có nghiệm đúng với mọi $x\in \left[ -1;9 \right]$ khi và chỉ khi ${{m}^{2}}-3m\le 16{{\left( \dfrac{1}{2} \right)}^{t}}-\left( {{t}^{2}}+2t-8 \right){{\left( \dfrac{2}{3} \right)}^{t}}$ có nghiệm đúng với $t\in \left[ -4;2 \right]$
${{m}^{2}}-3m\le \underset{t\in \left[ -4;2 \right]}{\mathop{\min }} g\left( t \right)$ với $g\left( t \right)=16{{\left( \dfrac{1}{2} \right)}^{t}}-\left( {{t}^{2}}+2t-8 \right){{\left( \dfrac{2}{3} \right)}^{t}}$
Ta có $h\left( x \right)=16{{\left( \dfrac{1}{2} \right)}^{t}}$ là hàm nghịch biến nên $h\left( x \right)\ge h\left( 2 \right)=4$ với $t\in \left[ -4;2 \right]$.
Ta có ${{t}^{2}}+2t-8\le 0$ với $t\in \left[ -4;2 \right]$ nên $u\left( t \right)=-\left( {{t}^{2}}+2t-8 \right){{\left( \dfrac{2}{3} \right)}^{t}}\ge 0=u\left( 2 \right)=u\left( -4 \right)$ với $t\in \left[ -4;2 \right]$.
Nên $g\left( t \right)\ge 4=g\left( 2 \right),\forall t\in \left[ -4;2 \right]\Rightarrow \underset{t\in \left[ -4;2 \right]}{\mathop{\min }} g\left( t \right)=g\left( 2 \right)=4$.
Khi đó ${{m}^{2}}-3m\le g\left( 2 \right)=4\Leftrightarrow -1\le m\le 4$.
$\Leftrightarrow 16{{\left( \dfrac{1}{2} \right)}^{f\left( x \right)}}-\left[ {{f}^{2}}\left( x \right)+2f\left( x \right)-8 \right]{{\left( \dfrac{2}{3} \right)}^{f\left( x \right)}}\ge {{m}^{2}}-3m$
Đặt $t=f\left( x \right)$, từ đồ thị ta thấy được $-4\le f\left( x \right)\le 2$ $\Rightarrow t\in \left[ -4;2 \right]$.
Để ${{16.3}^{f\left( x \right)}}-\left[ {{f}^{2}}\left( x \right)+2f\left( x \right)-8 \right]{{4}^{f\left( x \right)}}\ge \left( {{m}^{2}}-3m \right){{6}^{f\left( x \right)}}$ có nghiệm đúng với mọi $x\in \left[ -1;9 \right]$ khi và chỉ khi ${{m}^{2}}-3m\le 16{{\left( \dfrac{1}{2} \right)}^{t}}-\left( {{t}^{2}}+2t-8 \right){{\left( \dfrac{2}{3} \right)}^{t}}$ có nghiệm đúng với $t\in \left[ -4;2 \right]$
${{m}^{2}}-3m\le \underset{t\in \left[ -4;2 \right]}{\mathop{\min }} g\left( t \right)$ với $g\left( t \right)=16{{\left( \dfrac{1}{2} \right)}^{t}}-\left( {{t}^{2}}+2t-8 \right){{\left( \dfrac{2}{3} \right)}^{t}}$
Ta có $h\left( x \right)=16{{\left( \dfrac{1}{2} \right)}^{t}}$ là hàm nghịch biến nên $h\left( x \right)\ge h\left( 2 \right)=4$ với $t\in \left[ -4;2 \right]$.
Ta có ${{t}^{2}}+2t-8\le 0$ với $t\in \left[ -4;2 \right]$ nên $u\left( t \right)=-\left( {{t}^{2}}+2t-8 \right){{\left( \dfrac{2}{3} \right)}^{t}}\ge 0=u\left( 2 \right)=u\left( -4 \right)$ với $t\in \left[ -4;2 \right]$.
Nên $g\left( t \right)\ge 4=g\left( 2 \right),\forall t\in \left[ -4;2 \right]\Rightarrow \underset{t\in \left[ -4;2 \right]}{\mathop{\min }} g\left( t \right)=g\left( 2 \right)=4$.
Khi đó ${{m}^{2}}-3m\le g\left( 2 \right)=4\Leftrightarrow -1\le m\le 4$.
Đáp án A.
