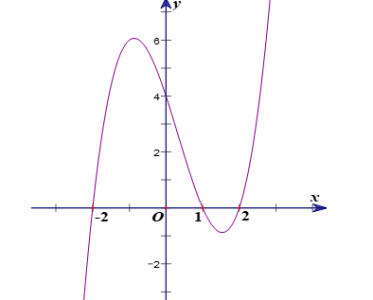
Cho hàm số $y=f\left( x \right)$ có đồ thị của $y={f}'\left( 3-2x...

Vì $g\left( x \right)=f\left( \left| {{x}^{3}}+2023x \right|+m \right)$ là hàm số chẵn nên số điểm cực trị của $g\left( x \right)$ bằng $2$ lần số cực trị dương của $f\left( {{x}^{3}}+2023x+m \right)$ cộng với $1.$
Với $x>0,$ ta có $g\left( x \right)=f\left( {{x}^{3}}+2023x+m \right);$ ${g}'\left( x \right)=\left( 3{{x}^{2}}+2023 \right){f}'\left( {{x}^{3}}+2023x+m \right).$
Đặt $x=3-2t$ ta có $t=\dfrac{3-x}{2}$ và ${f}'\left( x \right)={f}'\left( 3-2t \right)=0\Leftrightarrow \left[ \begin{aligned}
& t=\pm 2 \\
& t=1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=7 \\
& x=1 \\
& x=-1 \\
\end{aligned} \right..$
Suy ra ${g}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& {{x}^{3}}+2023x+m=7 \\
& {{x}^{3}}+2023x+m=1 \\
& {{x}^{3}}+2023x+m=-1 \\
\end{aligned} \right. $ $ \Leftrightarrow \left[ \begin{aligned}
& {{x}^{3}}+2023x=7-m(1) \\
& {{x}^{3}}+2023x=1-m(2) \\
& {{x}^{3}}+2023x=-1-m(3) \\
\end{aligned} \right..$
Hàm số $g\left( x \right)$ có ít nhất $5$ điểm cực trị khi và chỉ khi có ít nhất $2$ trong $3$ phương trình $(1),$ $(2),$ $(3)$ có nghiệm dương.
Xét hàm số $h\left( x \right)={{x}^{3}}+2023x$ có ${h}'\left( x \right)=3{{x}^{2}}+2023$.
Ta có bảng biến thiên của $h\left( x \right)$ như sau:
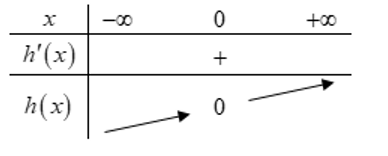Vì $7-m>1-m>-1-m$ nên ta có $1-m>0\Leftrightarrow m<1.$
Mà $m\in \left[ -2023;2023 \right]\cap \mathbb{Z}$ nên $m\in \left\{ -2023;...;0 \right\}.$
Vậy có $2024$ giá trị nguyên $m$ thỏa mãn yêu cầu bài toán.