Cho hàm số $f(x)=x^3+a x^2+b x+c$. Nếu phương trình $f(x)=0$ có ba...

Ta có: $f(x)=x^3+a x^2+b x+c$
$
\begin{aligned}
& f^{\prime}(x)=3 x^2+2 a x+b \\
& f^{\prime \prime}(x)=6 x+2 a \\
& f^{\prime \prime \prime}(x)=6
\end{aligned}
$
Gọi ba nghiệm của phương trình $f(x)=0$ lần lượt là $a ; b ; c$
$
\begin{gathered}
\text { Đặt } h(x)=2 f(x) \cdot f^{\prime \prime}(x)-\left(f^{\prime}(x)\right)^2 \\
h^{\prime}(x)=2 f^{\prime}(x) \cdot f^{\prime \prime}(x)+2 f(x) \cdot f^{\prime \prime \prime}(x)-2 f^{\prime}(x) \cdot f^{\prime \prime}(x) \\
=2 f(x) \cdot f^{\prime \prime \prime}(x)=12 \cdot f(x) \\
h^{\prime}(x)=0 \Leftrightarrow f(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=a \\
x=b \\
x=c
\end{array}\right.
\end{gathered}
$
Ta có bảng biến thiên của hàm số $h(x)$ :
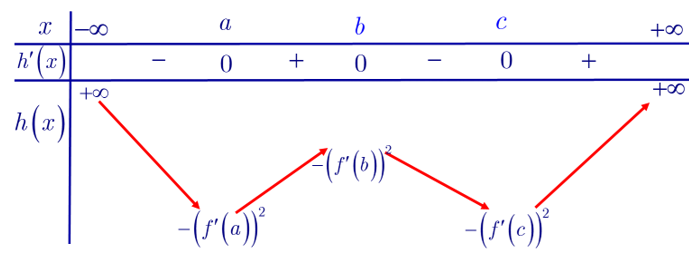Lại có phương trình $f(x)=0$ có ba nghiệm thực phân biệt $a ; b ; c \Rightarrow f(b)=0 \Leftrightarrow f^{\prime}(b) \neq 0 \Rightarrow$ $-\left(f^{\prime}(b)\right)^2<0$
Khi đó ta có bảng biến thiên của hàm số $h(x)$ :
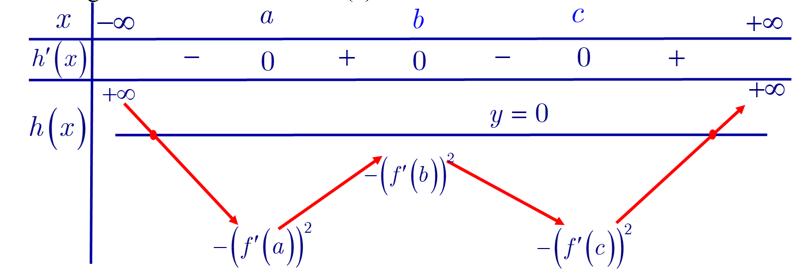Từ bảng biến thiên phương trình $h(x)=0$ có hai nghiệm phân biệt hay $2 f(x) \cdot f^{\prime \prime}(x)=\left[f^{\prime}(x)\right]^2$ có hai nghiệm phân biệt.