Google
Câu hỏi: Cho hàm số $f(x)$ có đạo hàm $f^{\prime}(x)=(x-1)^2\left(x^2-2 x\right)$ với mọi $x \in \mathbb{R}$. Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $g(x)=f\left(x^2-8 x+m\right)$ có 5 điểm cực trị?
A. 15 .
B. 16 .
C. 17
D. 18 .
A. 15 .
B. 16 .
C. 17
D. 18 .
Theo đề ra, ta có $g(x)=f\left(x^2-8 x+m\right) \Rightarrow g^{\prime}(x)=(2 x-8) f^{\prime}\left(x^2-8 x+m\right)$.
$
g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=4 \\
f^{\prime}\left(x^2-8 x+m\right)=0
\end{array}\right.
$
Đặt $t=x^2-8 x+m$, ta có phương trình $f^{\prime}\left(x^2-8 x+m\right)=0$ trở thành phương trình $f^{\prime}(t)=0$. Mà ta có $f^{\prime}(x)=(x-1)^2\left(x^2-2 x\right)$ nên $f^{\prime}(t)=(t-1)^2\left(t^2-2 t\right)$.
$
\begin{aligned}
& f^{\prime}(t)=0 \Rightarrow\left[\begin{array}{l}
t=1 \\
t=0 \\
t=2
\end{array}\right. \\
& \text { Vì } t=x^2-8 x+m \text { nên ta có: } \\
& t=1 \Leftrightarrow x^2-8 x+m=1 \Leftrightarrow x^2-8 x=1-m(1) ; \\
& t=0 \Leftrightarrow x^2-8 x+m=0 \Leftrightarrow x^2-8 x=-m(2) ; \\
& t=2 \Leftrightarrow x^2-8 x+m=2 \Leftrightarrow x^2-8 x=2-m(3) .
\end{aligned}
$
Ta có các nhận xét sau:
Vì $t=1$ là nghiệm bội chẵn nên phương trình (1) nếu có nghiệm thì nghiệm của nó cũng là nghiệm bội chẵn;
Do đó, hàm số không có điểm cực trị tại các nghiệm của phương trình (1);
Với mọi giá trị $m, 3$ phương trình trên, không có phương nào, có nghiệm trùng với nghiệm của một trong 2 phương trình còn lại.
Mặt khác, ta có nghiệm của phương trình (2) và (3) lần lượt là hoành độ giao điểm của đồ thị hàm số $h(x)=x^2-8 x$ với đường thẳng $y=-m$ và $y=2-m$.
Đặt $h(x)=x^2-8 x$, ta có:
Tập xác định $D=\mathbb{R}$.
$h^{\prime}(x)=2 x-8, h^{\prime}(x)=0 \Rightarrow x=4$, và $h(4)=-16$.
Ta có bảng biến thiên và đồ thị của hàm số $h(x)$ như sau:
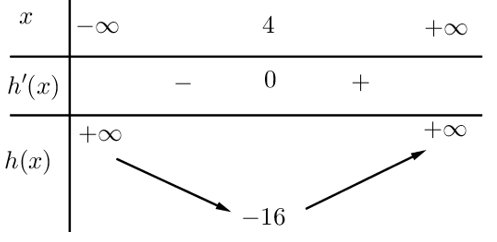
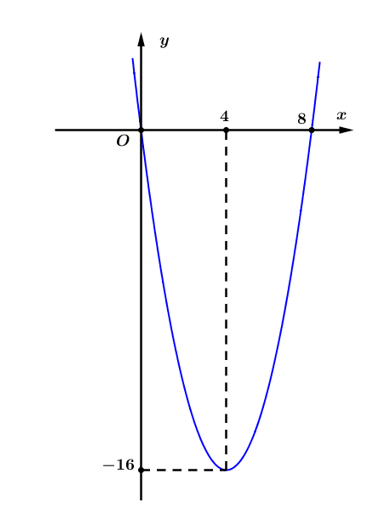Dựa vào đồ thị trên, ta thấy phương trình (2) và (3) nếu có 2 nghiệm phân biệt thì nghiệm của nó luôn luôn khác 4.
Vậy, hàm số $g(x)=f\left(x^2-8 x+m\right)$ có 5 điểm cực trị khi và chỉ khi phương trình (2) và (3) mỗi phương trình có 2 nghiệm phân biệt.
Dựa vào đồ thị hàm số ở trên, ta thấy giá trị của tham số $m$ để phương trình (2) và (3) có 2 nghiệm phân biệt là $\left\{\begin{array}{l}-m>-16 \\ 2-m>-16\end{array} \Leftrightarrow\left\{\begin{array}{l}m<16 \\ m<18\end{array} \Leftrightarrow m<16\right.\right.$.
Vậy, có 15 giá trị nguyên dương của tham số $m$ thỏa yêu cầu bài toán.
$
g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=4 \\
f^{\prime}\left(x^2-8 x+m\right)=0
\end{array}\right.
$
Đặt $t=x^2-8 x+m$, ta có phương trình $f^{\prime}\left(x^2-8 x+m\right)=0$ trở thành phương trình $f^{\prime}(t)=0$. Mà ta có $f^{\prime}(x)=(x-1)^2\left(x^2-2 x\right)$ nên $f^{\prime}(t)=(t-1)^2\left(t^2-2 t\right)$.
$
\begin{aligned}
& f^{\prime}(t)=0 \Rightarrow\left[\begin{array}{l}
t=1 \\
t=0 \\
t=2
\end{array}\right. \\
& \text { Vì } t=x^2-8 x+m \text { nên ta có: } \\
& t=1 \Leftrightarrow x^2-8 x+m=1 \Leftrightarrow x^2-8 x=1-m(1) ; \\
& t=0 \Leftrightarrow x^2-8 x+m=0 \Leftrightarrow x^2-8 x=-m(2) ; \\
& t=2 \Leftrightarrow x^2-8 x+m=2 \Leftrightarrow x^2-8 x=2-m(3) .
\end{aligned}
$
Ta có các nhận xét sau:
Vì $t=1$ là nghiệm bội chẵn nên phương trình (1) nếu có nghiệm thì nghiệm của nó cũng là nghiệm bội chẵn;
Do đó, hàm số không có điểm cực trị tại các nghiệm của phương trình (1);
Với mọi giá trị $m, 3$ phương trình trên, không có phương nào, có nghiệm trùng với nghiệm của một trong 2 phương trình còn lại.
Mặt khác, ta có nghiệm của phương trình (2) và (3) lần lượt là hoành độ giao điểm của đồ thị hàm số $h(x)=x^2-8 x$ với đường thẳng $y=-m$ và $y=2-m$.
Đặt $h(x)=x^2-8 x$, ta có:
Tập xác định $D=\mathbb{R}$.
$h^{\prime}(x)=2 x-8, h^{\prime}(x)=0 \Rightarrow x=4$, và $h(4)=-16$.
Ta có bảng biến thiên và đồ thị của hàm số $h(x)$ như sau:
Vậy, hàm số $g(x)=f\left(x^2-8 x+m\right)$ có 5 điểm cực trị khi và chỉ khi phương trình (2) và (3) mỗi phương trình có 2 nghiệm phân biệt.
Dựa vào đồ thị hàm số ở trên, ta thấy giá trị của tham số $m$ để phương trình (2) và (3) có 2 nghiệm phân biệt là $\left\{\begin{array}{l}-m>-16 \\ 2-m>-16\end{array} \Leftrightarrow\left\{\begin{array}{l}m<16 \\ m<18\end{array} \Leftrightarrow m<16\right.\right.$.
Vậy, có 15 giá trị nguyên dương của tham số $m$ thỏa yêu cầu bài toán.
Đáp án A.