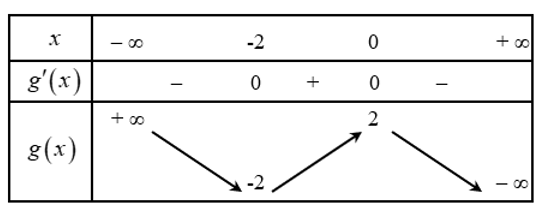
Cho hàm số bậc ba $y=f\left( x \right)$. Hàm số $g\left( x...

Từ giả thiết thì hàm số $f\left( x \right)$ sẽ có bảng biến thiên như sau:
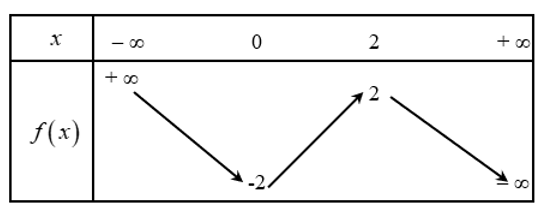Dựa vào bảng biến thiên suy ra $f\left( x \right)=-{{x}^{3}}+3{{x}^{2}}-2$.
Phương trình $f\left( x \right)=-{{x}^{3}}+3{{x}^{2}}-2=0\left[ \begin{aligned}
& x=1\pm \sqrt{3} \\
& x=1 \\
\end{aligned} \right.$
Phương trình $\sqrt{4+m{{x}^{2}}}.f\left( f\left( x \right)-m \right)=0 \left( * \right)$ với điều kiện $:4+m{{x}^{2}}\ge 0$.
Xét phương trình $f\left( f\left( x \right)-m \right)=0\Leftrightarrow \left[ \begin{aligned}
& f\left( x \right)-m=1-\sqrt{3} \\
& f\left( x \right)-m=1+\sqrt{3} \\
& f\left( x \right)-m=1 \\
\end{aligned} \right.$
Trường hợp 1: Nếu $m\ge 0$, ta có $\sqrt{4+m{{x}^{2}}}\ge 2$.
Khi đó ta có: $\left[ \begin{aligned}
& f\left( x \right)-m=1-\sqrt{3} \\
& f\left( x \right)-m=1+\sqrt{3} \\
& f\left( x \right)-m=1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& f\left( x \right)+\sqrt{3}=m+1 \left( 1 \right) \\
& f\left( x \right)-\sqrt{3}=m+1 \left( 2 \right) \\
& f\left( x \right)=m+1 \left( 3 \right) \\
\end{aligned} \right.$
Phác họa ba đồ thị trên cùng một hệ trục tọa độ:
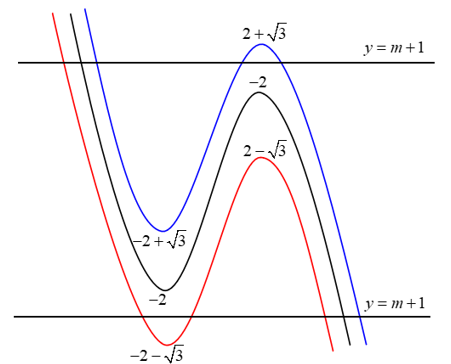Yêu cầu bài toán $\Leftrightarrow \left[ \begin{aligned}
& -2-\sqrt{3}<m+1<-2 \\
& 2<m+1<2+\sqrt{3} \\
\end{aligned} \right. $ mà $ m\ge 0\Rightarrow 1<m<1+\sqrt{3}\xrightarrow{m\in \mathbb{Z}}m=2$.
Trường hợp 2: Nếu $m<0$, $4+m{{x}^{2}}\ge 0\Leftrightarrow 4\ge -m{{x}^{2}}\Leftrightarrow {{x}^{2}}\le -\dfrac{4}{m}\Leftrightarrow \dfrac{-2}{\sqrt{-m}}\le x\le \dfrac{2}{\sqrt{-m}}$.
Nhận xét: Phương trình luôn có hai nghiệm là $x=\pm \dfrac{2}{\sqrt{-m}}$ khi đó bài toán trở thành tìm giá trị của tham số $m$ (với $m<0, m\in \mathbb{Z}$ ) sao cho phương trình $f\left( f\left( x \right)-m \right)=0$ có ba nghiệm phân biệt thuộc $\left( -\dfrac{2}{\sqrt{-m}};\dfrac{2}{\sqrt{-m}} \right)$.
Khi đó ta có: $\left[ \begin{aligned}
& f\left( x \right)-m=1-\sqrt{3}=-0,732 \\
& f\left( x \right)-m=1+\sqrt{3}=2,732 \\
& f\left( x \right)-m=1 \\
\end{aligned} \right.$
Do $m\in \mathbb{Z}$ nên xét $m\le -1$ suy ra $\left( -\dfrac{2}{\sqrt{-m}};\dfrac{2}{\sqrt{-m}} \right)\subset \left( 2;2 \right)$ nên trên khoảng $\left( -\dfrac{2}{\sqrt{-m}};\dfrac{2}{\sqrt{-m}} \right)$ có đúng một cực trị là $x=0$. Ta có: $f\left( x \right)-m=-{{x}^{3}}+3{{x}^{2}}-2-m$. Đặt $h\left( x \right)=f\left( x \right)-m$
Bảng biến thiên:
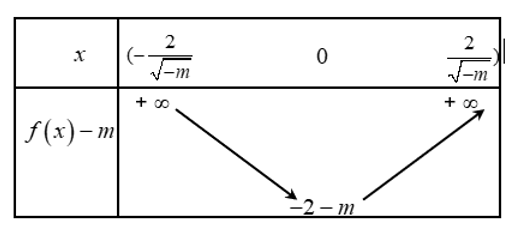Với $m=-1\Rightarrow h\left( x \right)=-{{x}^{3}}+3{{x}^{2}}-1\Rightarrow $ phương trình $f\left( h\left( x \right) \right)=0$ có $6$ nghiệm. Suy ra phương trình đã cho có $8$ nghiệm (loại)
Với $m=-2\Rightarrow h\left( x \right)=-{{x}^{3}}+3{{x}^{2}}\Rightarrow $ phương trình $f\left( h\left( x \right) \right)=0$ có $4$ nghiệm. Suy ra phương trình đã cho có $6$ nghiệm (loại)
Với $m=-3\Rightarrow h\left( x \right)=-{{x}^{3}}+3{{x}^{2}}+1\Rightarrow $ phương trình $f\left( h\left( x \right) \right)=0$ có $3$ nghiệm $\in \left( -\dfrac{2}{\sqrt{3}};\dfrac{2}{\sqrt{3}} \right)$. Suy ra phương trình đã cho có $5$ nghiệm (thỏa mãn).
Với $m\le -4\Rightarrow $ phương trình $f\left( h\left( x \right) \right)=0$ có tối đa $2$ nghiệm $\in \left( -\dfrac{2}{\sqrt{-m}};\dfrac{2}{\sqrt{m}} \right)$ (loại)
Vậy $m\in \!\!\{\!\!\text{ 2;} -\text{3 }\!\!\}\!\!$ nên tổng các giá trị nguyên của tham số $m$ bằng $-1$.