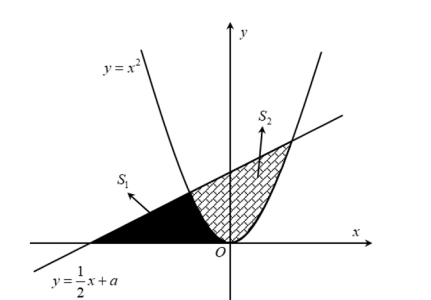
Câu hỏi: Cho đường thẳng $y=\dfrac{1}{2}x+a$ và parabol $y={{x}^{2}}$ ( $a$ là tham số thực). Gọi ${{S}_{1}},{{S}_{2}}$ lần lượt là diện tích của hai hình phẳng được tô đậm và gạch chéo trong hình vẽ bên. Khi ${{S}_{1}}={{S}_{2}}$ thì $a$ thuộc khoảng nào dưới đây?
A. $\left( \dfrac{7}{2};4 \right)$.
B. $\left( -\dfrac{1}{16};\dfrac{5}{2} \right)$.
C. $\left( \dfrac{5}{2};3 \right)$.
D. $\left( 3;\dfrac{7}{2} \right)$.
A. $\left( \dfrac{7}{2};4 \right)$.
B. $\left( -\dfrac{1}{16};\dfrac{5}{2} \right)$.
C. $\left( \dfrac{5}{2};3 \right)$.
D. $\left( 3;\dfrac{7}{2} \right)$.
Phương trình hoành độ giao điểm của của hai đồ thị: $\dfrac{1}{2}x+a={{x}^{2}}\Leftrightarrow 2{{x}^{2}}-x-2a=0$
Theo giả thiết, phương trình có hai nghiệm phân biệt $\Leftrightarrow \Delta =1+16a>0\Leftrightarrow a>-\dfrac{1}{16}$
Khi đó, phương trình có hai nghiệm ${{x}_{1}},{{x}_{2}} \left( {{x}_{1}}<{{x}_{2}} \right)$ thỏa: $\left\{ \begin{aligned}
& S={{x}_{1}}+{{x}_{2}}=\dfrac{1}{2} \\
& P={{x}_{1}}+{{x}_{2}}=-a \\
\end{aligned} \right.$
Diện tích hình phẳng: ${{S}_{1}}=\int_{-2a}^{{{x}_{1}}}{\left( \dfrac{x}{2}+a \right)}dx+\int_{{{x}_{1}}}^{0}{{{x}^{2}}dx}=\left. \left( \dfrac{{{x}^{2}}}{4}+ax \right) \right|_{-2a}^{{{x}_{1}}}+\left. \dfrac{{{x}^{3}}}{3} \right|_{{{x}_{1}}}^{0}$
$=\dfrac{1}{4}x_{1}^{2}+a{{x}_{1}}-\dfrac{1}{4}.4{{a}^{2}}+2{{a}^{2}}-\dfrac{1}{3}x_{1}^{3}=-\dfrac{1}{3}x_{1}^{3}+\dfrac{1}{4}x_{1}^{2}+a{{x}_{1}}+{{a}^{2}}$
Diện tích hình phẳng ${{S}_{2}}=\int_{{{x}_{1}}}^{{{x}_{2}}}{\left( \dfrac{1}{2}x+a-{{x}^{2}} \right)dx}=\dfrac{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}}{6}$
Theo giả thiết, ${{S}_{1}}={{S}_{2}}\Leftrightarrow \dfrac{1}{4}\left( x_{1}^{2}-4{{a}^{2}} \right)+a\left( {{x}_{1}}+2a \right)-\dfrac{x_{1}^{3}}{3}=\dfrac{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}}{6}$
$\Leftrightarrow -\dfrac{1}{6}\left( x_{1}^{3}+x_{2}^{3} \right)+\dfrac{1}{2}{{x}_{1}}.{{x}_{2}}\left( {{x}_{2}}-{{x}_{1}} \right)+\dfrac{x_{1}^{2}}{4}+a.{{x}_{1}}+{{a}^{2}}=0$
$\Leftrightarrow -\dfrac{1}{6}\left( \dfrac{1}{8}+\dfrac{3a}{2} \right)-\dfrac{a}{2}\sqrt{\dfrac{1}{4}+4a}+\dfrac{{{\left( 1-\sqrt{1+16a} \right)}^{2}}}{64}+a.\dfrac{1-\sqrt{1+16a}}{4}+{{a}^{2}}=0$ $\Rightarrow a\simeq 3,684$
Theo giả thiết, phương trình có hai nghiệm phân biệt $\Leftrightarrow \Delta =1+16a>0\Leftrightarrow a>-\dfrac{1}{16}$
Khi đó, phương trình có hai nghiệm ${{x}_{1}},{{x}_{2}} \left( {{x}_{1}}<{{x}_{2}} \right)$ thỏa: $\left\{ \begin{aligned}
& S={{x}_{1}}+{{x}_{2}}=\dfrac{1}{2} \\
& P={{x}_{1}}+{{x}_{2}}=-a \\
\end{aligned} \right.$
Diện tích hình phẳng: ${{S}_{1}}=\int_{-2a}^{{{x}_{1}}}{\left( \dfrac{x}{2}+a \right)}dx+\int_{{{x}_{1}}}^{0}{{{x}^{2}}dx}=\left. \left( \dfrac{{{x}^{2}}}{4}+ax \right) \right|_{-2a}^{{{x}_{1}}}+\left. \dfrac{{{x}^{3}}}{3} \right|_{{{x}_{1}}}^{0}$
$=\dfrac{1}{4}x_{1}^{2}+a{{x}_{1}}-\dfrac{1}{4}.4{{a}^{2}}+2{{a}^{2}}-\dfrac{1}{3}x_{1}^{3}=-\dfrac{1}{3}x_{1}^{3}+\dfrac{1}{4}x_{1}^{2}+a{{x}_{1}}+{{a}^{2}}$
Diện tích hình phẳng ${{S}_{2}}=\int_{{{x}_{1}}}^{{{x}_{2}}}{\left( \dfrac{1}{2}x+a-{{x}^{2}} \right)dx}=\dfrac{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}}{6}$
Theo giả thiết, ${{S}_{1}}={{S}_{2}}\Leftrightarrow \dfrac{1}{4}\left( x_{1}^{2}-4{{a}^{2}} \right)+a\left( {{x}_{1}}+2a \right)-\dfrac{x_{1}^{3}}{3}=\dfrac{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}}{6}$
$\Leftrightarrow -\dfrac{1}{6}\left( x_{1}^{3}+x_{2}^{3} \right)+\dfrac{1}{2}{{x}_{1}}.{{x}_{2}}\left( {{x}_{2}}-{{x}_{1}} \right)+\dfrac{x_{1}^{2}}{4}+a.{{x}_{1}}+{{a}^{2}}=0$
$\Leftrightarrow -\dfrac{1}{6}\left( \dfrac{1}{8}+\dfrac{3a}{2} \right)-\dfrac{a}{2}\sqrt{\dfrac{1}{4}+4a}+\dfrac{{{\left( 1-\sqrt{1+16a} \right)}^{2}}}{64}+a.\dfrac{1-\sqrt{1+16a}}{4}+{{a}^{2}}=0$ $\Rightarrow a\simeq 3,684$
Đáp án A.