Google
Câu hỏi: Cho các số phức ${{z}_{1}},{{z}_{2}}$ thỏa mãn $\begin{array}{*{35}{l}}
\left| {{z}_{1}}-2+i \right|=\left| {{{\bar{z}}}_{1}}+1-2i \right|\text{ v }\!\!\grave{\mathrm{a}}\!\!\text{ }\dfrac{1-{{z}_{2}}}{1+i} & \\
\end{array} $là số thuần ảo. Tìm giá trị nhỏ nhất của biếu thức $ P=\left|z_1-z_2\right|+\left|z_1-5+5 i\right|+\left|z_2-5+5 i\right|$.
A. ${{P}_{\text{min }}}=\sqrt{58}.$
B. ${{P}_{\text{min }}}=8.$
C. ${{P}_{\text{min }}}=2\sqrt{14}.$
D. ${{P}_{\min }}=\sqrt{57}.$
\left| {{z}_{1}}-2+i \right|=\left| {{{\bar{z}}}_{1}}+1-2i \right|\text{ v }\!\!\grave{\mathrm{a}}\!\!\text{ }\dfrac{1-{{z}_{2}}}{1+i} & \\
\end{array} $là số thuần ảo. Tìm giá trị nhỏ nhất của biếu thức $ P=\left|z_1-z_2\right|+\left|z_1-5+5 i\right|+\left|z_2-5+5 i\right|$.
A. ${{P}_{\text{min }}}=\sqrt{58}.$
B. ${{P}_{\text{min }}}=8.$
C. ${{P}_{\text{min }}}=2\sqrt{14}.$
D. ${{P}_{\min }}=\sqrt{57}.$
Đặt ${{z}_{1}}={{x}_{1}}+{{y}_{1}}i,\left( {{x}_{1}},{{y}_{1}}\in \mathbb{R} \right)\Rightarrow {{M}_{1}}=\left( {{x}_{1}};{{y}_{1}} \right).$
Ta có $\left\{ \begin{aligned}
& {{z}_{1}}-2+i={{x}_{1}}-2+\left( {{y}_{1}}+1 \right)i \\
& {{{\bar{z}}}_{1}}+1-2i={{x}_{1}}+1-\left( {{y}_{1}}+2 \right)i \\
\end{aligned} \right.\Rightarrow \left| {{z}_{1}}-2+i \right|=\left| {{{\bar{z}}}_{1}}+1-2i \right|\Rightarrow {{\left| {{z}_{1}}-2+i \right|}^{2}}={{\left| {{{\bar{z}}}_{1}}+1-2i \right|}^{2}}$
$\Rightarrow {{\left( {{x}_{1}}-2 \right)}^{2}}+{{\left( {{y}_{1}}+1 \right)}^{2}}={{\left( {{x}_{1}}+1 \right)}^{2}}+{{\left( {{y}_{1}}+2 \right)}^{2}}\Leftrightarrow 3{{x}_{1}}+{{y}_{1}}=0,\left( {{\Delta }_{1}} \right).$
Đặt ${{z}_{2}}={{x}_{2}}+{{y}_{2}}i,\left( {{x}_{2}},{{y}_{2}}\in \mathbb{R} \right)\Rightarrow {{M}_{2}}\left( {{x}_{2}};{{y}_{2}} \right).$
Ta có $\dfrac{1-{{z}_{2}}}{1+i}=\dfrac{\left( 1-{{x}_{2}}-{{y}_{2}}i \right)\left( 1-i \right)}{2}=\dfrac{1-{{x}_{2}}-{{y}_{2}}}{2}+mi,\left( m\in \mathbb{R} \right).$
Do $\dfrac{1-{{z}_{2}}}{1+i}$ là số thuần ảo ${{x}_{2}}+{{y}_{1}}-1=0,\left( {{\Delta }_{2}} \right).$
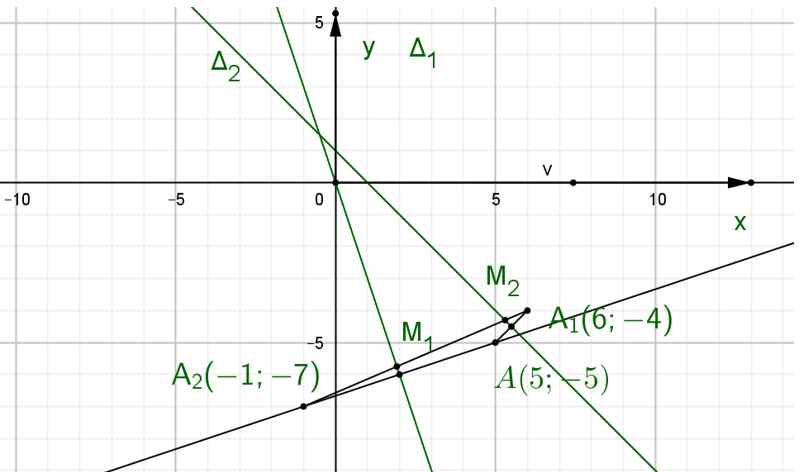Gọi ${{{A}_{1}}}$ là điểm đối xứng với $A\left( 5;-5 \right)$ qua ${{\Delta }_{2}}\Rightarrow {{A}_{1}}\left( 6;-4 \right).$
Gọi ${{{A}_{2}}}$ là điểm đối xứng với $A\left( 5;-5 \right)$ qua ${{\Delta }_{1}}\Rightarrow {{A}_{2}}\left( -1;-7 \right).$
$P=\left| {{z}_{1}}-{{z}_{2}} \right|+\left| {{z}_{1}}-5+5i \right|+\left| {{z}_{2}}-5+5i \right|={{M}_{1}}{{M}_{2}}+A{{M}_{1}}+A{{M}_{2}}={{M}_{1}}{{M}_{2}}+{{A}_{1}}M+{{A}_{2}}N\ge {{A}_{1}}{{A}_{2}}=\sqrt{58}.$
Ta có $\left\{ \begin{aligned}
& {{z}_{1}}-2+i={{x}_{1}}-2+\left( {{y}_{1}}+1 \right)i \\
& {{{\bar{z}}}_{1}}+1-2i={{x}_{1}}+1-\left( {{y}_{1}}+2 \right)i \\
\end{aligned} \right.\Rightarrow \left| {{z}_{1}}-2+i \right|=\left| {{{\bar{z}}}_{1}}+1-2i \right|\Rightarrow {{\left| {{z}_{1}}-2+i \right|}^{2}}={{\left| {{{\bar{z}}}_{1}}+1-2i \right|}^{2}}$
$\Rightarrow {{\left( {{x}_{1}}-2 \right)}^{2}}+{{\left( {{y}_{1}}+1 \right)}^{2}}={{\left( {{x}_{1}}+1 \right)}^{2}}+{{\left( {{y}_{1}}+2 \right)}^{2}}\Leftrightarrow 3{{x}_{1}}+{{y}_{1}}=0,\left( {{\Delta }_{1}} \right).$
Đặt ${{z}_{2}}={{x}_{2}}+{{y}_{2}}i,\left( {{x}_{2}},{{y}_{2}}\in \mathbb{R} \right)\Rightarrow {{M}_{2}}\left( {{x}_{2}};{{y}_{2}} \right).$
Ta có $\dfrac{1-{{z}_{2}}}{1+i}=\dfrac{\left( 1-{{x}_{2}}-{{y}_{2}}i \right)\left( 1-i \right)}{2}=\dfrac{1-{{x}_{2}}-{{y}_{2}}}{2}+mi,\left( m\in \mathbb{R} \right).$
Do $\dfrac{1-{{z}_{2}}}{1+i}$ là số thuần ảo ${{x}_{2}}+{{y}_{1}}-1=0,\left( {{\Delta }_{2}} \right).$
Gọi ${{{A}_{2}}}$ là điểm đối xứng với $A\left( 5;-5 \right)$ qua ${{\Delta }_{1}}\Rightarrow {{A}_{2}}\left( -1;-7 \right).$
$P=\left| {{z}_{1}}-{{z}_{2}} \right|+\left| {{z}_{1}}-5+5i \right|+\left| {{z}_{2}}-5+5i \right|={{M}_{1}}{{M}_{2}}+A{{M}_{1}}+A{{M}_{2}}={{M}_{1}}{{M}_{2}}+{{A}_{1}}M+{{A}_{2}}N\ge {{A}_{1}}{{A}_{2}}=\sqrt{58}.$
Đáp án A.