Google
Câu hỏi: Cho $a, b$ là hai số thực dương. Gọi $(\mathrm{H})$ là hình phẳng giới hạn bởi parabol $y=a x^2$ và đường thẳng $y=-b x$. Quay $(\mathrm{H})$ quanh trục hoành thu được khối có thể tích là $V_1$, quay $(\mathrm{H})$ quanh trục tung thu được khối có thể tích là $V_2$. Tìm $b$ sao cho $V_1=V_2$.
A. $b=\dfrac{5}{4}$.
B. $b=\dfrac{5}{3}$.
C. $b=\dfrac{5}{2}$.
D. $b=\dfrac{5}{6}$.
Phương trình hoành độ giao điểm của parabol và đường thẳng đã cho là $a x^2=-b x$.
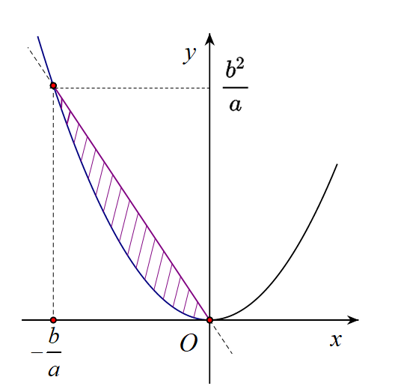
Do $a x^2=-b x \Leftrightarrow\left[\begin{array}{l}x=0 \\ x=-\dfrac{b}{a} \text { nên các giao điểm là } O \text { và } M\left(-\dfrac{b}{a} ; \dfrac{b^2}{a}\right)\end{array}\right.$
(Tham khảo hình vẽ kèm theo)
Đến đây ta có:
$+V_1=\pi \int_{-\dfrac{b}{a}}^0(-b x)^2 d x-\pi \int_{-\dfrac{b}{a}}^0\left(a x^2\right)^2 d x=\left.\pi b^2 \cdot \dfrac{x^3}{3}\right|_{-\dfrac{b}{a}} ^0-\left.\pi a^2 \cdot \dfrac{x^5}{5}\right|_{-\dfrac{b}{a}} ^0=\dfrac{2 \pi b^5}{15 a^3}$ (đơn vị thể tích).
$+V_2=\pi \int_0^{\dfrac{b^2}{a}}\left(-\sqrt{\dfrac{y}{a}}\right)^2 d y-\pi \int_0^{\dfrac{b^2}{a}}\left(-\dfrac{y}{b}\right)^2 d y=\left.\pi \dfrac{y^2}{2 a}\right|_0 ^{\dfrac{b^2}{a}}-\left.\pi \dfrac{y^3}{3 b^2}\right|_0 ^{\dfrac{b^2}{a}}=\dfrac{\pi b^4}{6 a^3}$ (đơn vị thể tích)
Do vậy $V_1=V_2 \Leftrightarrow \dfrac{2 \pi b^5}{15 a^3}=\dfrac{\pi b^4}{6 a^3} \Leftrightarrow b=\dfrac{5}{4}$.
A. $b=\dfrac{5}{4}$.
B. $b=\dfrac{5}{3}$.
C. $b=\dfrac{5}{2}$.
D. $b=\dfrac{5}{6}$.
Do $a x^2=-b x \Leftrightarrow\left[\begin{array}{l}x=0 \\ x=-\dfrac{b}{a} \text { nên các giao điểm là } O \text { và } M\left(-\dfrac{b}{a} ; \dfrac{b^2}{a}\right)\end{array}\right.$
(Tham khảo hình vẽ kèm theo)
Đến đây ta có:
$+V_1=\pi \int_{-\dfrac{b}{a}}^0(-b x)^2 d x-\pi \int_{-\dfrac{b}{a}}^0\left(a x^2\right)^2 d x=\left.\pi b^2 \cdot \dfrac{x^3}{3}\right|_{-\dfrac{b}{a}} ^0-\left.\pi a^2 \cdot \dfrac{x^5}{5}\right|_{-\dfrac{b}{a}} ^0=\dfrac{2 \pi b^5}{15 a^3}$ (đơn vị thể tích).
$+V_2=\pi \int_0^{\dfrac{b^2}{a}}\left(-\sqrt{\dfrac{y}{a}}\right)^2 d y-\pi \int_0^{\dfrac{b^2}{a}}\left(-\dfrac{y}{b}\right)^2 d y=\left.\pi \dfrac{y^2}{2 a}\right|_0 ^{\dfrac{b^2}{a}}-\left.\pi \dfrac{y^3}{3 b^2}\right|_0 ^{\dfrac{b^2}{a}}=\dfrac{\pi b^4}{6 a^3}$ (đơn vị thể tích)
Do vậy $V_1=V_2 \Leftrightarrow \dfrac{2 \pi b^5}{15 a^3}=\dfrac{\pi b^4}{6 a^3} \Leftrightarrow b=\dfrac{5}{4}$.
Đáp án A.