Câu hỏi: Cho M và N lần lượt là trung điểm của các cạnh AB, A1D1 của hình hộp ABCD. A1B1C1D1.
a) Xác định giao điểm P và Q của mặt phẳng (CMN) với các đường thẳng B1C1 và DB1.
b) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\overrightarrow {AQ} \) qua các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) trong đó \(\overrightarrow b = \overrightarrow {AB} ,\overrightarrow c = \overrightarrow {A{\rm{D}}} ,\overrightarrow a = \overrightarrow {A{A_1}} \).
a) Xác định giao điểm P và Q của mặt phẳng (CMN) với các đường thẳng B1C1 và DB1.
b) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\overrightarrow {AQ} \) qua các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) trong đó \(\overrightarrow b = \overrightarrow {AB} ,\overrightarrow c = \overrightarrow {A{\rm{D}}} ,\overrightarrow a = \overrightarrow {A{A_1}} \).
Lời giải chi tiết
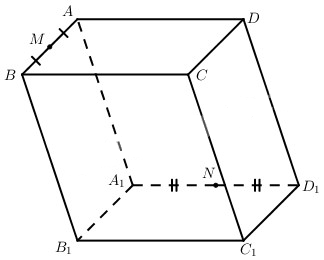
A) Đặt \(\overrightarrow {A{A_1}} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \).
P là giao điểm của mp(CMN) với đường thẳng B1C1 khi và chỉ khi C, M, N, P thuộc một mặt phẳng và P thuộc đường thẳng B1C1.
Ta có các điểm M, N, C, P thuộc một mặt phẳng nên tồn tại các số x, y, z sao cho:
\(x + y + z = 1 \left( * \right)\)
và \(\overrightarrow {AP} = x\overrightarrow {AM} + y\overrightarrow {AN} + z\overrightarrow {AC.} \)
Ta có:
\(\eqalign{ & \overrightarrow {AP} = x.{{\overrightarrow b } \over 2} + y\left( {\overrightarrow a + {{\overrightarrow c } \over 2}} \right) + z\left({\overrightarrow b + \overrightarrow c } \right) \cr & = y\overrightarrow a + \left({{x \over 2} + z} \right)\overrightarrow b + \left({{y \over 2} + z} \right)\overrightarrow c \left(1 \right) \cr} \)
Vì P thuộc đường thẳng B1C1 nên \(\overrightarrow {{B_1}P} = t\overrightarrow {{B_1}{C_1}} \), từ đó \(\overrightarrow {AP} = \overrightarrow b + \overrightarrow a +t \overrightarrow c \left( 2 \right)\)
Từ (1), (2) và do \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng nên
\(\left\{ \matrix{ y = 1 \hfill \cr {x \over 2} + z = 1 \hfill \cr {y \over 2} + z = t \hfill \cr} \right. \left( {**} \right)\)
Kết hợp (*) và (**), ta có:
\(\eqalign{ & \left\{ \matrix{ y = 1 \hfill \cr {x \over 2} + z = 1 \hfill \cr {y \over 2} + z = t \hfill \cr x + y + z = 1 \hfill \cr} \right. \cr & \Rightarrow z = - x \Rightarrow {x \over 2} - x = 1 \Leftrightarrow x = - 2 \cr & \Rightarrow z = 2, t = {5 \over 2} \cr} \)
Vậy giao điểm của mp(CMN) với đường thẳng B1C1 là điểm P xác định bời
\(\overrightarrow {{B_1}P} = {5 \over 2}\overrightarrow {{B_1}{C_1}} \) .
Tương tự như trên, nếu gọi Q là giao điểm của mp(CMN) với đường thẳng B1D thì ta có \(x + y + z = 1\).
và
\(\eqalign{ & \overrightarrow {AQ} = x\overrightarrow {AM} + y\overrightarrow {AN} + z\overrightarrow {AC} \cr & = y\overrightarrow a + \left( {{x \over 2} + z} \right)\overrightarrow b + \left({{y \over 2} + z} \right)\overrightarrow c \cr} \)
Mặt khác
\(\overrightarrow {AQ} = \overrightarrow b + \overrightarrow a + t\overrightarrow {{B_1}D}\)
\( = \overrightarrow a + \overrightarrow b + t\left( { - \overrightarrow a - \overrightarrow b + \overrightarrow c } \right) \)
\(= \left( {1 - t} \right)\overrightarrow a + \left({1 - t} \right)\overrightarrow b + t\overrightarrow c\)
Ta có hệ phương trình sau:
\(\eqalign{ & \left\{ \matrix{ y = 1 - t \hfill \cr {x \over 2} + z = 1 - t \hfill \cr {y \over 2} + z = t \hfill \cr x + y + z = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x \over 2} - y + z = 0 \hfill \cr x + y + z = 1 \hfill \cr {x \over 2} + {y \over 2} + 2{\rm{z}} = 1 \hfill \cr} \right. \cr & \Rightarrow 1 - z = 2 - 4{\rm{z}} \Leftrightarrow z = {1 \over 3} \cr & \Rightarrow x = {2 \over 9}, y = {4 \over 9}, t = {5 \over 9}. \cr} \)
Vậy giao điểm Q của đường thẳng B1D với mp(CMN) được xác định bởi
\(\overrightarrow {{B_1}Q} = {5 \over 9}\overrightarrow {{B_1}D} \)
b) Từ kết quả của câu a), ta có :
\(\eqalign{ & \overrightarrow {AP} = \overrightarrow a + \overrightarrow b + {5 \over 2}\overrightarrow c \cr & \overrightarrow {AQ} = {4 \over 9}\overrightarrow a + {4 \over 9}\overrightarrow b + {5 \over 9}\overrightarrow c \cr} \).
A) Đặt \(\overrightarrow {A{A_1}} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \).
P là giao điểm của mp(CMN) với đường thẳng B1C1 khi và chỉ khi C, M, N, P thuộc một mặt phẳng và P thuộc đường thẳng B1C1.
Ta có các điểm M, N, C, P thuộc một mặt phẳng nên tồn tại các số x, y, z sao cho:
\(x + y + z = 1 \left( * \right)\)
và \(\overrightarrow {AP} = x\overrightarrow {AM} + y\overrightarrow {AN} + z\overrightarrow {AC.} \)
Ta có:
\(\eqalign{ & \overrightarrow {AP} = x.{{\overrightarrow b } \over 2} + y\left( {\overrightarrow a + {{\overrightarrow c } \over 2}} \right) + z\left({\overrightarrow b + \overrightarrow c } \right) \cr & = y\overrightarrow a + \left({{x \over 2} + z} \right)\overrightarrow b + \left({{y \over 2} + z} \right)\overrightarrow c \left(1 \right) \cr} \)
Vì P thuộc đường thẳng B1C1 nên \(\overrightarrow {{B_1}P} = t\overrightarrow {{B_1}{C_1}} \), từ đó \(\overrightarrow {AP} = \overrightarrow b + \overrightarrow a +t \overrightarrow c \left( 2 \right)\)
Từ (1), (2) và do \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng nên
\(\left\{ \matrix{ y = 1 \hfill \cr {x \over 2} + z = 1 \hfill \cr {y \over 2} + z = t \hfill \cr} \right. \left( {**} \right)\)
Kết hợp (*) và (**), ta có:
\(\eqalign{ & \left\{ \matrix{ y = 1 \hfill \cr {x \over 2} + z = 1 \hfill \cr {y \over 2} + z = t \hfill \cr x + y + z = 1 \hfill \cr} \right. \cr & \Rightarrow z = - x \Rightarrow {x \over 2} - x = 1 \Leftrightarrow x = - 2 \cr & \Rightarrow z = 2, t = {5 \over 2} \cr} \)
Vậy giao điểm của mp(CMN) với đường thẳng B1C1 là điểm P xác định bời
\(\overrightarrow {{B_1}P} = {5 \over 2}\overrightarrow {{B_1}{C_1}} \) .
Tương tự như trên, nếu gọi Q là giao điểm của mp(CMN) với đường thẳng B1D thì ta có \(x + y + z = 1\).
và
\(\eqalign{ & \overrightarrow {AQ} = x\overrightarrow {AM} + y\overrightarrow {AN} + z\overrightarrow {AC} \cr & = y\overrightarrow a + \left( {{x \over 2} + z} \right)\overrightarrow b + \left({{y \over 2} + z} \right)\overrightarrow c \cr} \)
Mặt khác
\(\overrightarrow {AQ} = \overrightarrow b + \overrightarrow a + t\overrightarrow {{B_1}D}\)
\( = \overrightarrow a + \overrightarrow b + t\left( { - \overrightarrow a - \overrightarrow b + \overrightarrow c } \right) \)
\(= \left( {1 - t} \right)\overrightarrow a + \left({1 - t} \right)\overrightarrow b + t\overrightarrow c\)
Ta có hệ phương trình sau:
\(\eqalign{ & \left\{ \matrix{ y = 1 - t \hfill \cr {x \over 2} + z = 1 - t \hfill \cr {y \over 2} + z = t \hfill \cr x + y + z = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x \over 2} - y + z = 0 \hfill \cr x + y + z = 1 \hfill \cr {x \over 2} + {y \over 2} + 2{\rm{z}} = 1 \hfill \cr} \right. \cr & \Rightarrow 1 - z = 2 - 4{\rm{z}} \Leftrightarrow z = {1 \over 3} \cr & \Rightarrow x = {2 \over 9}, y = {4 \over 9}, t = {5 \over 9}. \cr} \)
Vậy giao điểm Q của đường thẳng B1D với mp(CMN) được xác định bởi
\(\overrightarrow {{B_1}Q} = {5 \over 9}\overrightarrow {{B_1}D} \)
b) Từ kết quả của câu a), ta có :
\(\eqalign{ & \overrightarrow {AP} = \overrightarrow a + \overrightarrow b + {5 \over 2}\overrightarrow c \cr & \overrightarrow {AQ} = {4 \over 9}\overrightarrow a + {4 \over 9}\overrightarrow b + {5 \over 9}\overrightarrow c \cr} \).