Câu hỏi: Cho hình chóp S. ABC có đáy là tam giác đều, SA = SB = SC = a và cùng tạo với mặt phẳng (ABC) góc 60°. Một mặt phẳng song song với hai cạnh chéo nhau của hình chóp và cắt hình chóp đó theo thiết diện là hình vuông. Tính diện tích thiết diện.
Lời giải chi tiết
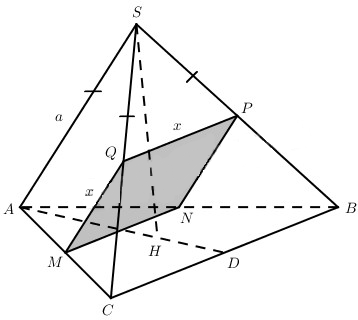
Giả sử H là tâm của tam giác đều.
Từ SA = SB = SC nên \(SH \bot \left( {ABC} \right)\) và \(\widehat {SAH} = {60^0}\).
Giả sử mặt phẳng song song với SA, CD và thiết diện thu được là hình vuông MNPQ.
Khi đó, nếu kí hiệu cạnh hình vuông là x thì:
\(\eqalign{ & {x \over {SA}} = {{CQ} \over {C{\rm{S}}}} \left( 1 \right) \cr & {x \over {BC}} = {{SQ} \over {SC}} \left(2 \right) \cr} \)
Từ (1), (2) suy ra:
\(\eqalign{ & x\left( {{1 \over {SA}} + {1 \over {BC}}} \right) = {{CQ + Q{\rm{S}}} \over {C{\rm{S}}}} = 1 \cr & \Rightarrow x= {{SA. BC} \over {SA + BC}} = {{a. BC} \over {a + BC}} \cr} \)
Mặt khác \(HA = SA\cos {60^0} = {a \over 2}\).
mà \(HA = {{BC\sqrt 3 } \over 3}\).
Suy ra \(BC = {{a\sqrt 3 } \over 2}\).
Từ đó \(x = {{a.{{a\sqrt 3 } \over 2}} \over {a + {{a\sqrt 3 } \over 2}}} = {{a\sqrt 3 } \over {2 + \sqrt 3 }} = a\sqrt 3 \left( {2 - \sqrt 3 } \right)\).
Vậy \({S_{MNPQ}} = {\left[ {a\sqrt 3 \left( {2 - \sqrt 3 } \right)} \right]^2} = 3{{\rm{a}}^2}{\left({2 - \sqrt 3 } \right)^2}\).
Giả sử H là tâm của tam giác đều.
Từ SA = SB = SC nên \(SH \bot \left( {ABC} \right)\) và \(\widehat {SAH} = {60^0}\).
Giả sử mặt phẳng song song với SA, CD và thiết diện thu được là hình vuông MNPQ.
Khi đó, nếu kí hiệu cạnh hình vuông là x thì:
\(\eqalign{ & {x \over {SA}} = {{CQ} \over {C{\rm{S}}}} \left( 1 \right) \cr & {x \over {BC}} = {{SQ} \over {SC}} \left(2 \right) \cr} \)
Từ (1), (2) suy ra:
\(\eqalign{ & x\left( {{1 \over {SA}} + {1 \over {BC}}} \right) = {{CQ + Q{\rm{S}}} \over {C{\rm{S}}}} = 1 \cr & \Rightarrow x= {{SA. BC} \over {SA + BC}} = {{a. BC} \over {a + BC}} \cr} \)
Mặt khác \(HA = SA\cos {60^0} = {a \over 2}\).
mà \(HA = {{BC\sqrt 3 } \over 3}\).
Suy ra \(BC = {{a\sqrt 3 } \over 2}\).
Từ đó \(x = {{a.{{a\sqrt 3 } \over 2}} \over {a + {{a\sqrt 3 } \over 2}}} = {{a\sqrt 3 } \over {2 + \sqrt 3 }} = a\sqrt 3 \left( {2 - \sqrt 3 } \right)\).
Vậy \({S_{MNPQ}} = {\left[ {a\sqrt 3 \left( {2 - \sqrt 3 } \right)} \right]^2} = 3{{\rm{a}}^2}{\left({2 - \sqrt 3 } \right)^2}\).