Câu hỏi: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc và AB = a, BC = b, CD = c.
a. Tính độ dài AD.
b. Chỉ ra điểm cách đều A, B, C, D
c. Tính góc giữa đường thẳng AD và mặt phẳng (BCD), góc giữa đường thẳng AD và mặt phẳng (ABC).
a. Tính độ dài AD.
b. Chỉ ra điểm cách đều A, B, C, D
c. Tính góc giữa đường thẳng AD và mặt phẳng (BCD), góc giữa đường thẳng AD và mặt phẳng (ABC).
Phương pháp giải
- Chứng minh \(\widehat {ABD} = \widehat {ACD} = {90^0}\).
a) Tính độ dài bằng cách sử dụng định lý Py-ta-go.
b) Xác định điểm cách đều bằng tính chất tam giác vuông.
c) Góc giữa đường thẳng và mặt phẳng (khác \({90^0}\)) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Lời giải chi tiết
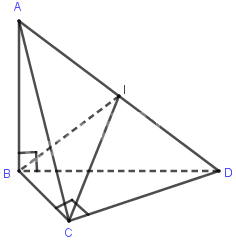
A. Ta có: CD ⊥ BC và CD ⊥ AB nên CD ⊥ (ABC)
mà AC ⊂ (ABC) do đó CD ⊥ AC.
Trong tam giác vuông ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)
Trong tam giác vuông ACD ta có:
\(A{D^2} = A{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\)
Suy ra: \(AD = \sqrt {{a^2} + {b^2} + {c^2}} \)
b. Ta có: \(AB \bot BC\) và \(AB \bot CD\) suy ra AB ⊥ (BCD) do đó AB ⊥ BD.
Gọi I là trung điểm AD ta có:
+) Tam giác ACD vuông tại C có CI là đường trung tuyến ứng với cạnh huyền AD nên: \(IA = IC = ID = \frac{{AD}}{2}\left( 1 \right)\)
+) Tam giác ABD vuông tại B có BI là đường trung tuyến ứng với cạnh huyền AD nên: $IA = IB = ID = \dfrac{{AD}}{2}\left( 2 \right)$
Từ (1) và (2) suy ra: IA = IB = IC = ID
Vây I cách đều A, B, C, D.
c. Ta có: \(AB \bot \left( {BCD} \right)\) \(\Rightarrow BD\) là hình chiếu của \(AD\) trên \(\left( {BCD} \right)\).
Khi đó góc \(\widehat {\left( {AD,\left( {BCD} \right)} \right)} = \widehat {\left({AD, BD} \right)} = \widehat {ADB}\).
Xét tam giác \(ABD\) vuông tại \(B\) thì \(\sin \widehat {ADB} = \dfrac{{AB}}{{AD}} = \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \(\Rightarrow \widehat {\left( {AD,\left( {BCD} \right)} \right)} = \arcsin \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Lại có \(DC \bot \left( {ABC} \right)\) \(\Rightarrow AC\) là hình chiếu của \(AD\) trên \(\left( {ABC} \right)\).
Khi đó góc \(\widehat {\left( {AD,\left( {ABC} \right)} \right)} = \widehat {\left({AD, AC} \right)} = \widehat {DAC}\)
Xét tam giác \(ACD\) vuông tại \(C\) thì \(\sin \widehat {DAC} = \dfrac{{CD}}{{AD}} = \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \(\Rightarrow \widehat {\left( {AD,\left( {ABC} \right)} \right)} = \arcsin \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
- Chứng minh \(\widehat {ABD} = \widehat {ACD} = {90^0}\).
a) Tính độ dài bằng cách sử dụng định lý Py-ta-go.
b) Xác định điểm cách đều bằng tính chất tam giác vuông.
c) Góc giữa đường thẳng và mặt phẳng (khác \({90^0}\)) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Lời giải chi tiết
A. Ta có: CD ⊥ BC và CD ⊥ AB nên CD ⊥ (ABC)
mà AC ⊂ (ABC) do đó CD ⊥ AC.
Trong tam giác vuông ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)
Trong tam giác vuông ACD ta có:
\(A{D^2} = A{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\)
Suy ra: \(AD = \sqrt {{a^2} + {b^2} + {c^2}} \)
b. Ta có: \(AB \bot BC\) và \(AB \bot CD\) suy ra AB ⊥ (BCD) do đó AB ⊥ BD.
Gọi I là trung điểm AD ta có:
+) Tam giác ACD vuông tại C có CI là đường trung tuyến ứng với cạnh huyền AD nên: \(IA = IC = ID = \frac{{AD}}{2}\left( 1 \right)\)
+) Tam giác ABD vuông tại B có BI là đường trung tuyến ứng với cạnh huyền AD nên: $IA = IB = ID = \dfrac{{AD}}{2}\left( 2 \right)$
Từ (1) và (2) suy ra: IA = IB = IC = ID
Vây I cách đều A, B, C, D.
c. Ta có: \(AB \bot \left( {BCD} \right)\) \(\Rightarrow BD\) là hình chiếu của \(AD\) trên \(\left( {BCD} \right)\).
Khi đó góc \(\widehat {\left( {AD,\left( {BCD} \right)} \right)} = \widehat {\left({AD, BD} \right)} = \widehat {ADB}\).
Xét tam giác \(ABD\) vuông tại \(B\) thì \(\sin \widehat {ADB} = \dfrac{{AB}}{{AD}} = \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \(\Rightarrow \widehat {\left( {AD,\left( {BCD} \right)} \right)} = \arcsin \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Lại có \(DC \bot \left( {ABC} \right)\) \(\Rightarrow AC\) là hình chiếu của \(AD\) trên \(\left( {ABC} \right)\).
Khi đó góc \(\widehat {\left( {AD,\left( {ABC} \right)} \right)} = \widehat {\left({AD, AC} \right)} = \widehat {DAC}\)
Xét tam giác \(ACD\) vuông tại \(C\) thì \(\sin \widehat {DAC} = \dfrac{{CD}}{{AD}} = \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \(\Rightarrow \widehat {\left( {AD,\left( {ABC} \right)} \right)} = \arcsin \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)