Câu hỏi: Chứng minh rằng \(\left| z \right| = \left| {\rm{w}} \right| = 1\) thì số \({{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\) là số thực (giả sử \(1 + z{\rm{w}} \ne 0\)).
Phương pháp giải
Sử dụng tính chất:
Số phức z=a+bi là số thực nếu \(\overline z = z\)
Lời giải chi tiết
Ta có \(z.\overline z = {\left| z \right|^2} = 1 \Rightarrow \overline z = {1 \over z}\). Tương tự \(\overline {\rm{w}} = {1 \over {\rm{w}}}\)
Do đó \(\overline {\left( {{{z + {\rm{w}}} \over {1 + z{\rm{w}}}}} \right)} = {{\overline z + \overline {\rm{w}} } \over {1 + \overline z .\overline {\rm{w}} }} = {{{1 \over z} + {1 \over {\rm{w}}}} \over {1 + {1 \over z}.{1 \over {\rm{w}}}}} = {{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\).
Suy ra \({{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\) là số thực.
Cách khác:
Giả sử z=a+bi, w=a'+b'i với a2+b2=a'2+b'2=1 và 1+zw ≠ 0
Vì |z| = 1 nên z. z−=1
Khi đó, ta có:
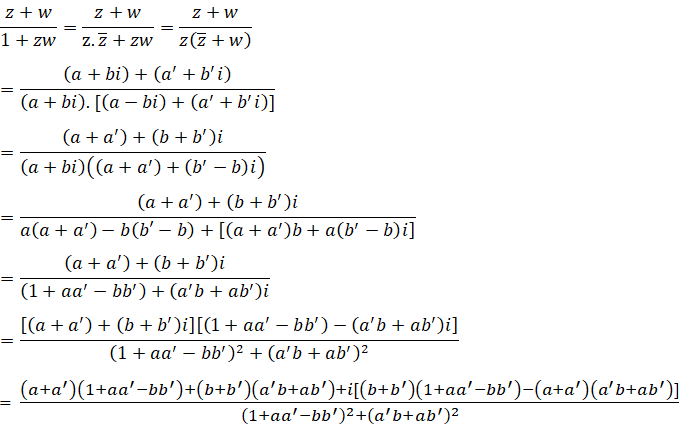
Xét phần ảo ở trên tử số ta có: (b+b')(1+aa'-bb')-(a+a')(a' b+ab')
=b+baa'-b2b'+b'+b' aa'-bb'2-aa' b-a2 b'-a'2 b-a'ab'
=b+b'-b' (a2+b2 )-b(b'2+a'2 )=b+b'-b'-b=0
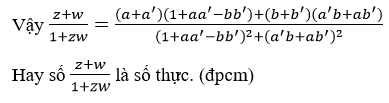
Sử dụng tính chất:
Số phức z=a+bi là số thực nếu \(\overline z = z\)
Lời giải chi tiết
Ta có \(z.\overline z = {\left| z \right|^2} = 1 \Rightarrow \overline z = {1 \over z}\). Tương tự \(\overline {\rm{w}} = {1 \over {\rm{w}}}\)
Do đó \(\overline {\left( {{{z + {\rm{w}}} \over {1 + z{\rm{w}}}}} \right)} = {{\overline z + \overline {\rm{w}} } \over {1 + \overline z .\overline {\rm{w}} }} = {{{1 \over z} + {1 \over {\rm{w}}}} \over {1 + {1 \over z}.{1 \over {\rm{w}}}}} = {{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\).
Suy ra \({{z + {\rm{w}}} \over {1 + z{\rm{w}}}}\) là số thực.
Cách khác:
Giả sử z=a+bi, w=a'+b'i với a2+b2=a'2+b'2=1 và 1+zw ≠ 0
Vì |z| = 1 nên z. z−=1
Khi đó, ta có:
Xét phần ảo ở trên tử số ta có: (b+b')(1+aa'-bb')-(a+a')(a' b+ab')
=b+baa'-b2b'+b'+b' aa'-bb'2-aa' b-a2 b'-a'2 b-a'ab'
=b+b'-b' (a2+b2 )-b(b'2+a'2 )=b+b'-b'-b=0