Câu hỏi: Cho đoạn thẳng \(AB\) và đường tròn \((C)\) tâm \(O\), bán kính \(r\) nằm về một phía của đường thẳng \(AB\). Lấy điểm \(M\) trên \((C)\), rồi dựng hình bình hành \(ABMM’\). Tìm tập hợp các điểm \(M’\) khi \(M\) di động trên \((C)\).
Phương pháp giải
Sử dụng định nghĩa: \(T_{\vec v}(M) = M' \Leftrightarrow \overrightarrow {MM'} = \vec v\).
Lời giải chi tiết
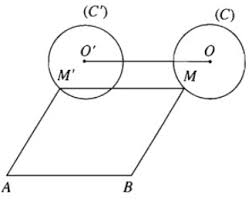
Do tứ giác \(ABMM’\) là hình bình hành nên \(\vec{BA}=\vec{MM’}\). Từ đó suy ra \(M’\) là ảnh của \(M\) qua phép tịnh tiến theo vectơ \(\vec{BA}\). Từ đó suy ra tập hợp các điểm \(M’\) là đường tròn \((C’)\), ảnh của \((C)\) qua phép tịnh tiến theo vectơ \(\vec {BA}\).
Sử dụng định nghĩa: \(T_{\vec v}(M) = M' \Leftrightarrow \overrightarrow {MM'} = \vec v\).
Lời giải chi tiết
Do tứ giác \(ABMM’\) là hình bình hành nên \(\vec{BA}=\vec{MM’}\). Từ đó suy ra \(M’\) là ảnh của \(M\) qua phép tịnh tiến theo vectơ \(\vec{BA}\). Từ đó suy ra tập hợp các điểm \(M’\) là đường tròn \((C’)\), ảnh của \((C)\) qua phép tịnh tiến theo vectơ \(\vec {BA}\).